
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
A Parallelogram PuzzleA while ago (March 2nd at 16:28 to be reasonably precise) Ed Southall asked a great question on Twitter:
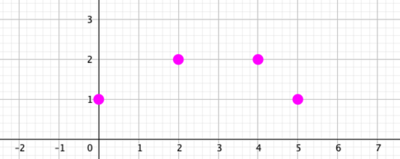
Here's the setup:
That's a pretty bold claim, and of late I've become less sure of myself about these sorts of things. More than once I've made a claim like that, only to have an underlying assumption exposed, leaving me to think more carefully. Which is good, though sometimes embarrassing, and sometimes even a little painful. So I wondered, are there really exactly two solutions? I invite you to go and read the thread, which I've extracted and drawn in chart form. There you will see some of the solutions, and some of the reasoning. But I promised I'd write more about my thinking, so here it is ...
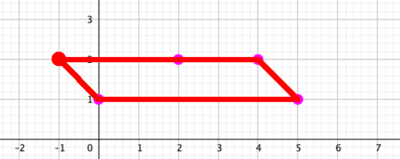
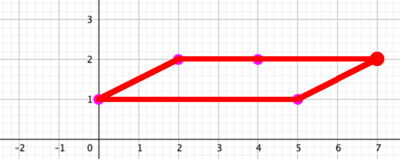
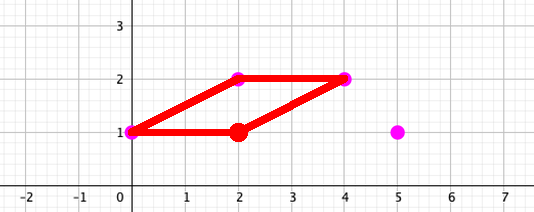
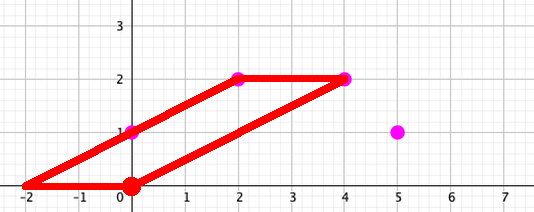
The first solutionsHere are two solutions:
I'm pretty sure there's no other way to:
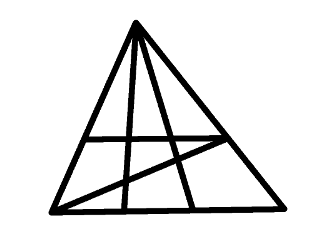
Starting to wonder ...But then I thought of this puzzle.
So let's go back and look at the original wording:
So maybe we don't have to involve all the dots, maybe we only need to have three of our original dots plus one extra, and require that they are the corners/vertices of our parallelogram. So maybe the question is:
So how many of these are there? OK, take any three points and label them A, B, and C. Assume that you are going around the parallelogram cyclically, and where does your next point have to be?
There are 24 ways to choose 3 points in order from 4, so there should be 24 solutions, assuming no repeats.
But wait! There's more!So now, what if our parallelogram just needs to "go through" the points, and the points don't necessarily have to be at the corners? For example, like this:
As you start to explore this you will find infinitely many solutions, but they will, perhaps, come in families, and perhaps you can start to describe those families and get a handle on what's going on.
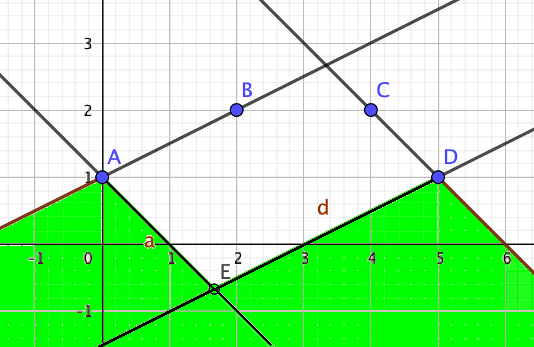
FeedbackColin Beveridge (Web site) has got in touch and sent me this diagram:
If point E is put anywhere in the green region(s) then we can construct a parallelogram that has all 5 points on the perimeter. It's not the convex hull, but it is a parallelogram that joins all the dots.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email