
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
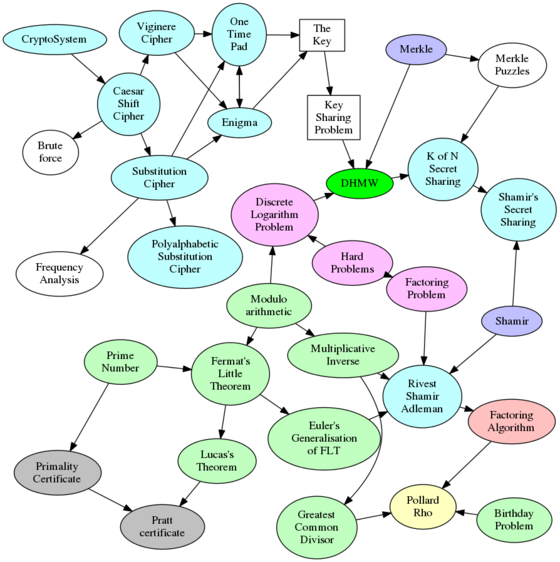
Crypto-Connections - 2019/04/30Having given the maths club talk last Saturday (which went very well) I was left with the preparative work that I'd done. That consists of lists of concepts, people, algorithms, cryptosystems, and some of the connections between them. Here is the diagram I ended up going with:
I started in the top left and talked about the Caesar Shift Cipher and how that can be broken quickly, even though in its day it was military grade encryption. Then the realisation that we're using one symbol instead of another, but why use this displacement by a constant? Hence the idea of a general substitution cipher. But that can be broken by frequency analysis, so we need to thwart that. We can do it in several ways: using more that one symbol for each letter in the plain text, interleaving different substitutions, and so on. But this is well-trodden ground. In the end we get to the idea that the key is the thing that we need to share, but which must be kept secret from everyone else. Easy enough to do if we can agree it in advance, but what if we can't meet, and can only communicate over an insecure channel? And so we arrived at Diffie-Hellman-Merkle-Williamson Key Exchange. To explain we took a quick diversion to talk about Modulo Arithmetic, the Discrete Logarithm Problem, and what we mean by a "Hard Problem". I deliberately finished a little early so the students could ask me anything about any of the remaining topics, and we finished with the Pollard Rho method of factoring integers, and how we can (sometimes) find factors without simply dividing by numbers until we find one that works. It was a good session, but I'm left with the collection of nodes and the connections between them. What should I do with that? I think it could be a brilliant resource, especially if each node points to a page or two that can explain that specific concept in depth. But it's currently incomplete, and I'm not really the one to finish it. So here's what I'm going to do. I'm going to create a wiki with one page per "bubble", and on each page put an annotation of its type ("Person", "Theorem", etc.) and some predicates indicating connections to other bubbles. People can then look at mining the wiki to create sub-graphs of interest. What do you think? Is that a potentially valuable project? Surely something like this already exists. It's tempting just to say "Use Wikipedia", but that's not really an answer. Wikipedia attempts to be an encyclopedia, and if you want to learn this sort of material, or get an overview, it's not a good resource. Is it good enough? Should there be something better? Is there already something better? Talk to me ...
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email