
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
What is "Big Oh"?So a brief recap:
This post is going to look at that carefully, because while it's true that if the "time taken" functions of two algorithms "look like" each other in the long run then they have the same time complexity, that's not enough. Algorithms can behave erratically, so the concept of "this looks like that" isn't really enough, we would like to do better.
So don't be too worried if some of the details don't make sense yet. The broad conclusion is this:
Not really linear, but sort of.
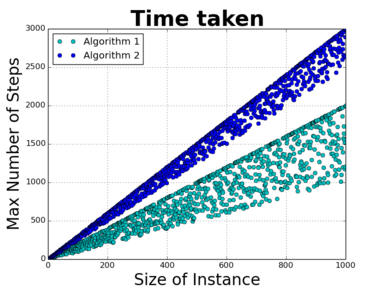
So let's have a look at the time-performance of two hypothetical algorithms on the same problem. They are different algorithms, and are quite complex, so their behaviours are not especially easy to understand. Even so, let's posit that they behave as shown in this chart. These two algorithms behave somewhat erratically, with some instance sizes taking much less than others, but broadly, both algorithms take time that grows linearly(ish) with the size of the instance. In some sense these two algorithms are behaving very similarly, and it would be great to have some way of capturing that mathematically. Then we remember two things:
Well in this case that's easy, we can just use $2^n$. That will certainly exceed our algorithm's run time. Hmm. Not really either helpful or informative. What we really want is the best upper bound. So here's what has been proven to be both useful and informative.
Getting an upper bound with "Domination"The concept we use is to think of one function "dominating" another. In formulas, we say that function $f(n)$ "dominates" function $g(n)$ if, after some time, $f(n)$ is always bigger than $g(n).$ OK, so that's not quite true. We allow for a constant, and we say something more precise about "in the long run" and we get this:
This isn't quite enough ... Suppose by way of an example that the time taken by algorithm $A$ is linear, so we can write $T_A(n)=kn$ for some constant $k$. Using our definition, it is true to say that this is dominated by $n^2,$ because it doesn't matter what $k$ might be, eventually $n^2$ will be bigger than $k\cdot{n}$. But that isn't really very helpful, and isn't as informative as we might like. By itself the definition of "to dominate" doesn't really capture how the algorithm behaves. In a sense it's not aggressive enough, it's too "loose". But an upper bound is an upper bound, and what we're really asking for is for the best known upper bound. That brings us to our final form. So the set-up is this. We have a problem, $P$, and for that problem we have an algorithm, $A$. At best we can we compute an upper bound for how long $A$ takes for each size of instance of $P$. We'll call that $T_A(n).$ For simple problems we might be able to compute that exactly, but for sufficiently complex problems we can usually only get an upper bound. Then we say this:
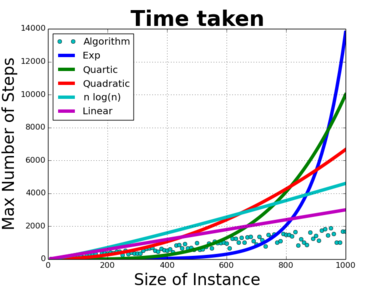
It's actually more complicated than that(now there's a surprise)So look again at the plot for our hypothetical algorithm, and overlay various functions that increase as $n$ increases. It's not helpful, I know, but it's true to say that the time function for this algorithm is dominated by $2^n$. It's substantially better to say that it's dominated by $n^4$, and it's better again to say it's dominated by $n^2$. Better still, it's dominated by $n\cdot\log(n)$. But it's also dominated by the function $f(n)=n$, and by $g(n)=n+5,$ and perhaps more surprisingly, by $h(n)=n-\log(n).$ What? Yes, believe it or not the function $f(n)=n$ is dominated by $n-\log(n)$. To see this, we look at the definition. That asks if there is a $k$ and an $N$ such that when $n>N$ we have $k(n-\log(n))>n.$ Rearranging that, we want to know if there is a $k$ such that when $n$ is big enough, $(k-1)n>k\log(n).$ But just taking $k=2$ suffices, so yes, $n$ is dominated by $n-\log(n)$. You might think that would render the whole concept sufficiently non-intuitive as to be useless, but actually it lets us find the idea of the "dominating term". In essence, $n$ grows faster than $\log(n)$, so including any terms that are essentially just $\log(n)$ doesn't change things. It's the fastest growing term that matters, the slower growing don't change things enough to make a difference.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email