Non Repeating Decimals

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

In the previous post we talked about repeating decimals, and showed that every (eventually) repeating decimal is a rational number, and every rational number has a (possibly trivial) (eventually) repeating decimal representation.

But what about non-repeating decimals? Firstly, are there such things as non-repeating decimals?

Well, yes. We can easily construct a non-repeating decimal as follows.

Write your decimal point, and the digit "1" with increasing an number of zeroes between them, like this:

0.1 0 1 00 1 000 1 0000 1 00000 1 000000 1 00...

(The spacing is just to make the construction easier to see)

The number of zeroes increases each time, and it's an interesting exercise to show that this sequence never falls into a repeating pattern.

"But wait!", I hear you cry. "That's just one! I want more "

OK, then let's make lots of non-repeating decimals.

Take the above decimal expansion and replace the zeroes with any digit other than one. Seriously, each 0 can be replaced by any digit other than 1. What you get is always a non-repeating decimal.

Which is nice.

"But wait!", I hear you cry. "These are artificial, somehow they feel unnatural."

Well, OK, let's look at this ...

Yes, I know the algebraic version, so please don't tell me about it. This is intended to give a different intuition.
Here's a short version, leaving out lots of steps. It's a rough summary of the whole post, so don't expect to follow this unless you're already familiar with all the concepts.
If you can't follow this, read the post, then come back to it.
If $\sqrt{2}$ is rational then we can construct two squares of integer size, one twice the area of the other. Take two of the smaller squares and overlay them on the larger. We observe that the uncovered area is equal to the double covered area, all of which are squares, thus giving a smaller example. Lather, rinse, repeat, and thus impossible.
Consider the square of side length $1$, also known as the unit square, and suppose, just suppose, that the diagonal is of rational length - say $\frac{a}{b}.$ We're going to derive an impossibility from this, so I'll keep coming back to it so we remember where this all started.

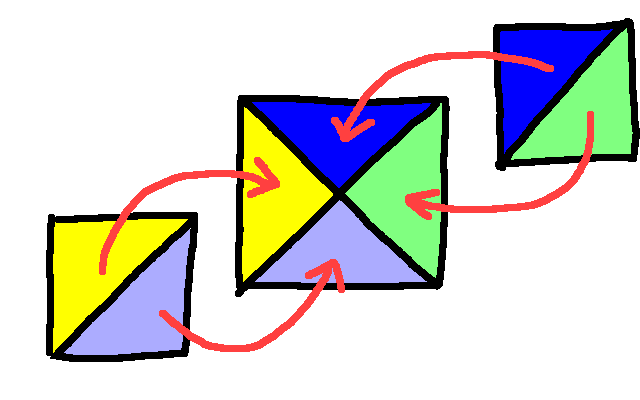
Firstly, let's multiply the size up by a factor of $b$, so now the side length is $b$, and the diagonal length is $a$. So we have a square of integer side length, and whose diagonal is also of integer length. Remember, we got that simply by assuming that the length of the diagonal of the unit square is rational.

If we take two copies of the square and cut each in half along the diagonal, we can assemble them to make a square of twice the area of the original, like this:

https://www.solipsys.co.uk/images/ConstructingOneSquareFromTwo.png

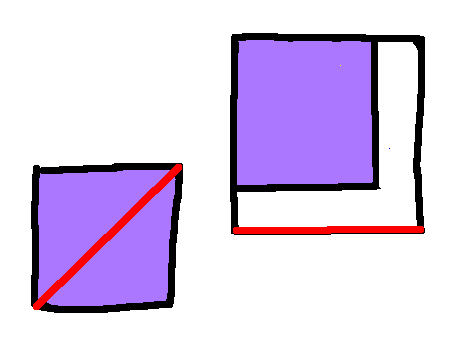
So now we have a larger square derived from our smaller square. Let's put the smaller square into the larger square:

https://www.solipsys.co.uk/images/SmallerSquareInLargerSquare.png

By construction, the lengths shown here in red are the same - the diagonal of the small square is the same as the length of the larger square, because that's how we made the larger square.

We know that the smaller square has to cover the mid-point, because if it didn't it would have to have area no more that 1/4 of the larger square, and it's area is 1/2 of it.

The area remaining - here in white - is the same area as the smaller square, but we can't cover it completely with another square, because it's the wrong shape. So we can put another square into the large square, and some parts will remain uncovered, while the central section will be double-covered:

https://www.solipsys.co.uk/images/OverlappingTwoSquaresInOne.png

The two smaller squares here are indicated with stripes in different directions, and we can see that the central section, which is a square, is double-covered, while there are two smaller squares that remain uncovered.

And again, we remember that the squares all having integer side-lengths relies solely on the diagonal of the unit square being rational.
We can work out their sizes based on the sizes of the original. Since everything is an integer, the sizes of these smaller squares, both the one in the middle and the ones in the corners, are the sums and differences of integers, and hence are also integers.

So we now have two copies of an integer sized square whose combined area is that of a single, larger, integer sized square. Cutting the smaller squares diagonally in half and rearranging them (as before), we can exactly cover the central, larger square. In doing so, the diagonals of the smaller squares become the edges of the larger square, and so we can see that the smaller squares have integer length diagonals.

Actually, we started with the unit square with rational diagonal and used that to get to an integer sized square with integer diagonal, but these two things are equivalent. Given either we can construct the other.
So we started with an integer sized square with integer diagonal, and we've constructed a smaller integer side-length square with integer diagonal, and there's nothing to stop us from repeating the process to get a smaller square, and a smaller one, and a smaller one, each with integer side-length and integer diagonal.

But that's impossible. We can't keep generating smaller and smaller positive integers.

Thus we've shown that it's impossible to have an integer sized square with an integer length diagonal, and so similarly impossible for the length of the diagonal of the unit square to be a rational.

Now take any square with an integer length side $S$. We know from Pythagoras that the diagonal is of length $\sqrt{2}{\cdot}S$, and we've just shown that it can never be an integer. If it could be a rational, say $a/b$, then we could simply multiple up by $b$ and the diagonal of the newer, scaled up square would be $a$, an integer. But that's impossible.

So for every integer $S$, the number $\sqrt{2}{\cdot}S$ is irrational, and that includes the case when $S=1$. Hence $\sqrt{2}$ is irrational.

From the previous blog post that means that the decimal expansion of $\sqrt{2}$ will continue forever and never repeat.

Acknowledgements

My thanks to several friends and colleagues for comments, questions, thoughts, and constructive feedback, all of which have made this post better. It's still not as good as I'd like, and I may yet re-write the entire thing. We'll see.

My commenters don't seem to want to be mentioned by name - I'll add names as and when I get permission.

<<<< Prev <<<<

Rational Repeats

>>>> Next >>>>

Waiting In Vain ...