
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
The "Up/Down" tides - 2019/03/28So while in orbit at about the altitude of the ISS we've looked at throwing a ball sideways, and we've looked at throwing a ball forwards or backwards. What happens if we throw the ball up? Or down? Is that different? Do we finally have the ball travel away in a straight line at a constant speed? What new horrors lie in store?
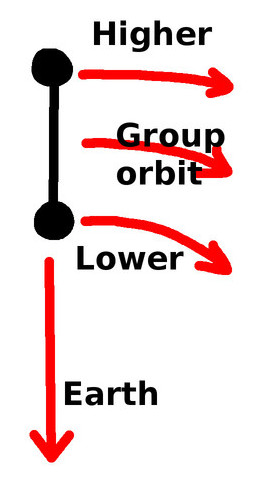
One way of thinking about this is to consider two equal masses tethered together by a 2 metre rope. We start with them in a "station keeping" configuration with the rope pointing at the Earth's centre. Let's think about each of these masses relative to their centre of gravity, which will be in the middle of the rope. The masses (and the rope, but we'll assume the rope is of negligible mass) can be thought of as a single system, and that system will orbit the Earth taking 92 minutes. But the "lower" mass, the one closer to the Earth, is, well, closer to the Earth. For that to have a stable orbit it would have to travel slightly faster than it is, so its speed isn't enough to keep it in a circular orbit. The result is that it tries to fall, The "upper" mass, by contrast, is travelling slightly faster than a circular orbit requires, so it will be trying to ascend, to rise away for the combined centre of gravity. So the two masses are trying to separate from each other, and the rope is in tension, holding them in their current positions. The result is that we see a "stretching" force in the "up/down" direction. That means that if you "throw" the ball downwards, or upwards, it will appear to accelerate away from you. How quickly? Good question ...
We're assuming the Earth is a perfect, homogeneous sphere of circumference exactly 40 million metres, and we're assuming that we're in an orbit taking exactly 92 minutes, which is 5520 seconds. We will also assume that $g$ is exactly $\pi^2$, which is pretty close. Under those assumptions, the radius of the orbit $D$ is 6,758,642 metres. We can compute the velocity as $2\pi D/5520$, which is 7,693 $ms^{-1}$. Out of interest, although we won't use it here, we can also compute the height of the orbit above the Earth's surface as about 392.445 kms. (In all these cases the level of precision quoted is unjustified, but we'll carry it for now. A proper error analysis is probably justified, but a little tedious for this post.) We are interested in the acceleration at our combined mass system orbital radius $D$ as compared with acceleration one metre below, or above. So we want
There are a couple of interesting consequences of this. One is this. Take a satellite that can be considered as two large lumps. Early satellites were powered by a form of nuclear power plant, so you could have the working part of the satellite and connect it via power cable to the power plant. Have that cable a few tens of metres long, and you'll end up with the satellite and power unit aligning themselves to have the cable pointing at the Earth. In this way you get some of the satellite's orientation "for free". Useful, provided you remember to arrange to have the satellite closer to the Earth and the power unit further. (Also, if the cable is a conductor then it can generate power as it cuts through the Earth's magnetic field, or, alternatively, power can be put through the cable to generate thrust. Although in each case, not a lot.) The second is that if you want two satellites flying in close formation, one "above" the other, then you either need to provide a constant inwards force on the outer one, or a constant outwards force on the inner one (or a bit of both). The size of the force depends on the distance between them, because the tidal force grows linearly with the distance. (Until it doesn't, because the approximations start to break down.) AcknowledgementsMy thanks to Bill Mullins (Twitter) for conversations about transfer orbits and more. I need to follow up further on some of his thoughts and suggestions.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email