
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
In the previous post we talked about repeating decimals, and showed
that every (eventually) repeating decimal is a rational number, and
every rational number has a (possibly trivial) (eventually) repeating
decimal representation.
But what about non-repeating decimals? Firstly, are there such things as non-repeating decimals? Well, yes. We can easily construct a non-repeating decimal as follows. Write your decimal point, and the digit "1" with increasing an number of zeroes between them, like this:
The number of zeroes increases each time, and it's an interesting exercise to show that this sequence never falls into a repeating pattern. "But wait!", I hear you cry. "That's just one! I want more " OK, then let's make lots of non-repeating decimals. Take the above decimal expansion and replace the zeroes with any digit other than one. Seriously, each 0 can be replaced by any digit other than 1. What you get is always a non-repeating decimal. Which is nice. "But wait!", I hear you cry. "These are artificial, somehow they feel unnatural." Well, OK, let's look at this ...
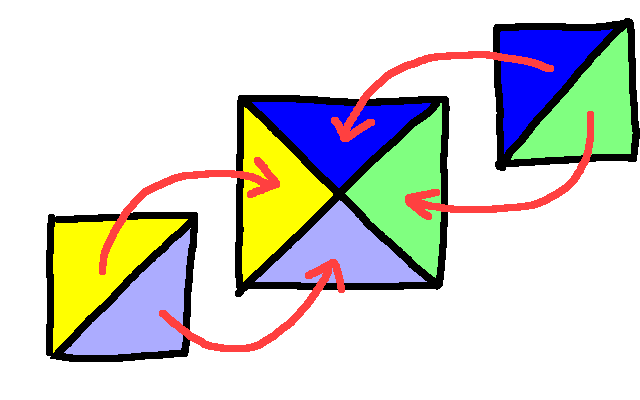
Firstly, let's multiply the size up by a factor of $b$, so now the side length is $b$, and the diagonal length is $a$. So we have a square of integer side length, and whose diagonal is also of integer length. Remember, we got that simply by assuming that the length of the diagonal of the unit square is rational. If we take two copies of the square and cut each in half along the diagonal, we can assemble them to make a square of twice the area of the original, like this:
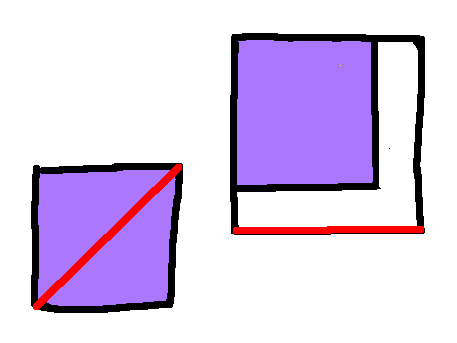
So now we have a larger square derived from our smaller square. Let's put the smaller square into the larger square:
By construction, the lengths shown here in red are the same - the diagonal of the small square is the same as the length of the larger square, because that's how we made the larger square. We know that the smaller square has to cover the mid-point, because if it didn't it would have to have area no more that 1/4 of the larger square, and it's area is 1/2 of it. The area remaining - here in white - is the same area as the smaller square, but we can't cover it completely with another square, because it's the wrong shape. So we can put another square into the large square, and some parts will remain uncovered, while the central section will be double-covered:
The two smaller squares here are indicated with stripes in different directions, and we can see that the central section, which is a square, is double-covered, while there are two smaller squares that remain uncovered.
So we now have two copies of an integer sized square whose combined area is that of a single, larger, integer sized square. Cutting the smaller squares diagonally in half and rearranging them (as before), we can exactly cover the central, larger square. In doing so, the diagonals of the smaller squares become the edges of the larger square, and so we can see that the smaller squares have integer length diagonals.
But that's impossible. We can't keep generating smaller and smaller positive integers. Thus we've shown that it's impossible to have an integer sized square with an integer length diagonal, and so similarly impossible for the length of the diagonal of the unit square to be a rational. Now take any square with an integer length side $S$. We know from Pythagoras that the diagonal is of length $\sqrt{2}{\cdot}S$, and we've just shown that it can never be an integer. If it could be a rational, say $a/b$, then we could simply multiple up by $b$ and the diagonal of the newer, scaled up square would be $a$, an integer. But that's impossible. So for every integer $S$, the number $\sqrt{2}{\cdot}S$ is irrational, and that includes the case when $S=1$. Hence $\sqrt{2}$ is irrational. From the previous blog post that means that the decimal expansion of $\sqrt{2}$ will continue forever and never repeat.
AcknowledgementsMy thanks to several friends and colleagues for comments, questions, thoughts, and constructive feedback, all of which have made this post better. It's still not as good as I'd like, and I may yet re-write the entire thing. We'll see. My commenters don't seem to want to be mentioned by name - I'll add names as and when I get permission.
Send us a comment ...
|


 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email