 Subscribe! Subscribe!

My latest posts can be
found here:
Previous blog posts:
Additionally, some earlier writings:
|
What is Graph Three-Colouring?
Here is something you may have seen before. Take a map, any map, and
colour the regions so that if two regions share a border, they must
get different colours.
Usually we count the exterior as a region and everything still holds.
Some people use the convenience of drawing a box and saying that they
don't care about anything outside it. Either is a choice, and it
doesn't make much difference.
So if we have only one region then clearly we colour it with whatever
colour we choose, and we only need one colour. If we have two regions
then they are going to touch somewhere, so they will have to get
different colours. Fair enough.
If we have a checkerboard sort of arrangement then we still only
need two colours, colouring them in the usual way. The black
squares only meet at a corner, and that's OK - they are not
sharing a boundary, so they don't need to be different colours.
We can choose to make them different, but that's different.
If you see what I mean.
So by creating bigger and bigger checkerboards we can make maps
of whatever size we like that can still be covered by just
two colours. We say that we can create "arbitrarily large"
two-colourable maps.
If all of that seems easy and obvious, here's an extra challenge.
Suppose we also have to colour the outside, bounding region. The
checkerboard pattern always has both colours on the squares on
the boundary, so we can't use one of those two colours for the
outside. That means that if we have to colour the outside as well,
the idea of larger and larger checkerboards no longer lets us
create arbitrarily large two-colourable maps, because the exterior
has to get a third colour.
Moving beyond the checkerboard ...
In fact, we can be more daring and more adventurous. We don't
have to have anything as simple as a tiling of the plane with
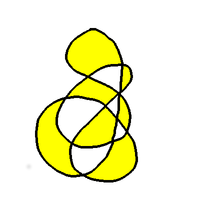
squares. Take any doodle made with a single pen stroke, and
ending up where it started. The resulting diagram can always
be coloured with just two colours.
This is what we'll call The Doodle Theorem, and we'll come
back to that in a little while.
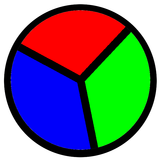
But sometimes things require three colours, a simple pie in
three pieces is an example. Indeed, if you decide that the
exterior also requires colouring, a pie into any number of
pieces greater than one requires at least three colours, and
sometimes four.
But one day back in the 1800s, De Morgan wrote:
|
|
"A student of mine [Guthrie] asked me to day
to give him a reason for a fact which I did
not know was a fact - and do not yet. He
says that if a figure be any how divided and
the compartments differently colored so that
figures with any portion of common boundary
line are differently colored - four colors
may be wanted but not more - the following
is his case in which four colors are wanted.
Query cannot a necessity for five or more be
invented ..."
|
|
And thus was born the Four Colour Conjecture.
But I'm not going to go into that here! There are many good
papers and books explaining the history, etc. Instead, I'm
off in a different direction.
Abstracting away from the map ...
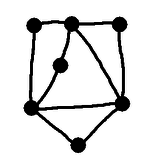
A map, with
watch-towers
|
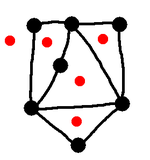
We mark the
capitals
|
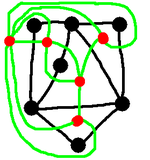
... and join them
with roads
|
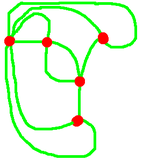
The dual graph
|
|
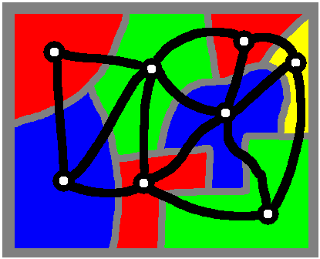
Let's look at our map. We are thinking, of course, of the regions
as countries, and the lines as borders between them. We then have
watchtowers wherever the borders meet, and sometimes on the border
as well. So we have regions, lines, and points. To use the
technical terms from graph theory, we have faces (although they
are still sometimes called regions), edges, and vertices.
So our map is a graph that can be drawn on the plane - it is a
planar graph.
Now let's do the following. Think of the regions as countries,
and mark on our map each of the capitals. If two countries
share a border, mark in a road joining the capitals. Don't put
any other roads, and don't have the roads cross each other. In
this way we have a new diagram of vertices (the capitals) and
edges (the roads).
We're also going to say that if a particular border has a watchtower in
the middle, or even more than one watchtower along its length, we will
put a road for each section of boundary. So two capitals may have more
than one road joining them.
This seems to be a useful idea, and we give it a name. Here we can see
a map, then we overlay onto it the capitals and the roads joining them,
and finally we erase the original map and get left with just the road
network. This final diagram is called the dual of the original.
If we can assign colours to the capitals (the vertices) such that each
road (edge) has a different colour at each end, then the countries can
inherit the capital's colour, and that gives us a colouring of the
original map. But in the same way, a valid colouring of the regions
induces a colouring of the capitals in such a way that any two capitals
(vertices) that are joined by a road (edge) must have different colours.
So colouring the original map is exactly the same task as colouring the
vertices in the dual.
"So what?" - you may think.
|
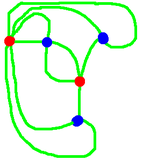
Colour the
capitals
|
Induced colouring
of the map
|
From Doodle
to dual
to colouring
|
Leaving the plane behind
Why are we doing this? What's wrong with talking about colouring maps?
When we colour the regions on a map we are specifically limited to
working on (or in) the two-dimensional surface. But when we are talking
about graphs we are no longer limited to a surface. We can talk
about graphs in abstract.
So let's return, as promised, to what we call The Doodle Theorem.
We claim that a map drawn with a single pen stroke that returns to
its starting point can be two-coloured. A proof goes roughly like
this:
- Take a planar graph that's been drawn with a single pen stroke
that returns to its starting point.
- Such a graph is said to have an "Euler Cycle".
- At every vertex we go in, and then out, so
- Every vertex must have an even number of edges.
- In the dual, a circuit around a vertex of the original will
have an even number of edges,
- ... because each edge in the dual crosses an edge in the original.
- Extend that, and we can show that every circuit has an
even number of edges.
- Note: This requires a bit of proof!
- A graph is bipartite if and only if every circuit is even.
- This also requires a bit of proof.
None of that is obvious! That's why this has the status of a theorem,
and you can read more about it here: The Doodle Theorem.
So the dual is bipartite, and that means it can be bi-coloured! So the
dual can be bi-coloured, and that corresponds to a bi-colouring of the
original map.
And we're done - a planar graph with an Euler Cycle can be bi-coloured.
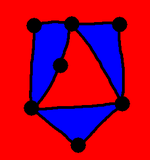
Bi-Partite graphs
A map and
its dual
|
It's pretty clear that a bi-partite graph can be two coloured, but if
you're given a graph, how easy or hard is it to decide if it's
bi-partite?
Easy. Really easy.
To decide if a graph is bi-partite, pick one vertex, colour it red.
Colour its neighbours green, colour their neighbours red, and just
keep going. If the graph is bi-partite this never goes wrong. If
it goes wrong, it's not bipartite. And that's it!
But this map is not bi-colourable - the dual is not bi-partite. So
given a graph it's really easy to tell if it's bi-partite or not, is
the same true of tri-partite-ness?
Given a graph, can we easily tell if it's tri-partite?
No.
What?
What about tri-partite?
|
Here we are talking about colouring the vertices - we have
now left behind the idea of colouring regions in maps - that's too
limiting, because it's restricted to graphs/maps that can be drawn
in the plane (or other two-dimensional surface). |
Well, to be tri-partite is the same as being three-colourable, because
a three-colouring gives us a division of the vertices into three sets
where the edges are only ever between the sets, never within. So to
ask if a graph is tri-partite is to ask if it is three colourable.
And it turns out that this is thought to be hard. You may notice that
I say "thought to be". The thing is - no one knows if it really is
hard. What currently is known is this:
- We don't know of any algorithm that can efficiently
determine if a graph is three-colourable.
Of course, we need to define what we mean by "efficient," but we can
do that. What's more, this is a question that is worth a million
dollars. Literally. It's one of the Millennium Problems to determine
if there is, or if there is not, an efficient algorithm for solving
the three-colouring problem.
To get a deeper understanding of this, we can look at
Factoring Via Graph Three Colouring. There we can see, explicitly, that
a problem thought to be hard can in fact be solved, provide we can
three-colour efficiently. But here's a flavour.
Three-colouring a graph
|
Given a graph, an independent set is a set of vertices that
have no edges between them. |
We can three-colour a graph if we can find an independent set of
vertices such that the remaining graph is bi-partite. Given an
independent set it's trivial (as shown above) to decide if the
remaining graph forms a bipartite graph, so it comes down to finding
independent sets. And given a set, it's trivial to decide if it's
independent. So we can find any possible three-colourings by
- Find a subset of vertices, then
- if it's independent,
- if the remainder is bipartite,
- you've found a three-colouring.
But if you have $N$ vertices in your graph, there are $2^N$ possible
subsets, so this algorithm is terribly inefficient.
Problem is, every algorithm we know is inefficient - there is no
known algorithm that takes time that is polynomial in the number
of vertices.
Comments
I've decided no longer to include comments directly via the Disqus
(or any other) system. Instead, I'd be more than delighted to get
emails from people who wish to make comments or engage in discussion.
Comments will then be integrated into the page as and when they are
appropriate.
If the number of emails/comments gets too large to handle then I
might return to a semi-automated system. That's looking increasingly
unlikely.
|









 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email