
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
As an experiment, we can punch "10" into a calculator and take the square root. Given that we're starting with a number that's bigger than 1, it's no real surprise that we get a smaller number. In fact, we get 3.16227766... We can take the square root of that, and we get 1.77827941... Now, if you actively like numbers, you may think that that is quite close to one and seven ninths, or $1\frac{7}{9}$. If we write that as an "improper fraction" it's $16/9$. And the fun thing about $16/9$ is that both $16$ and $9$ are squares, so if we take the square root again we should get something very close to $4/3$. And we do - we get 1.333521432... Winding this backwards, and squaring up $4/3$ multiple times, we can see why this happens. Taking $\left(\frac{4}{3}\right)^8$ we get $65536/6561$, which is very close to 10. We can continue the process to see if anything new and interesting happens, and it's not too long before our numbers are basically one plus a little bit of small rubbish.
So, if we plot the result against how many times we've taken a square root it looks like this:
Ignoring the first few terms we get this:
That's interesting. To have a closer look at this we can generate a table of the rubbish when we have small powers. So for a small power of $x$ we plot compute $10^x$. The table is shown here at left, and we can see, as expected, we're getting one plus small rubbish. Now let's subtract off the one and see what we've got. Best seen in a plot:
It's a straight line! Well, nearly a straight line. So it looks like when the power is small, when $x$ is small, the value of $10^x$ is 1 plus rubbish, where the rubbish is a multiple of the power. So when $x$ is small, there is a constant $c$ such that:
So the process of taking repeated square roots, looking at the rubbish, and comparing with the power, has given us a constant, and in this case if we measure the constant we get an answer of around 2.302585... But I say "in this case" because we started with 10, and we can wonder whether we get a different answer if we start with, say, 5 instead. So we can go through the process again, this time starting with 5, and we end up again with a straight line graph, but the slope is different! This time the slope is about 1.6094379...
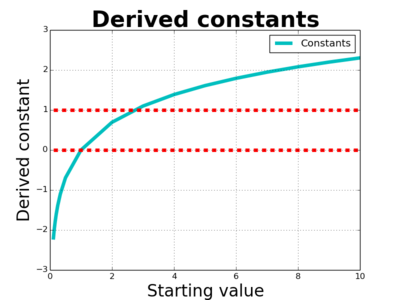
So how can we fill in more values? Well, given a starting value $S$, we're asking for a constant, $c$, such that when $x$ is really small, the value of $S^x$ is roughly $1+cx$. Here is a plot of the rubbish for starting values of 2, 3, 5, and 10:
So for each starting value we want to compute the constant. To do so - at least approximately - we pick some small number $x$ to use as a power, something like one millionth. Then for each starting number, $S$, we compute $\frac{1}{x}(S^x-1)$. We've got the first couple of values, and now we can fill them in:
So if X times Y equals Z, maybe, just maybe, the constants for X and Y add to give the constant for Z. Why would that be? But that's not the direction I'm going. Instead, notice that the constants are growing:
I've included starting with some values less than one, as well as the value for one itself, and now we can see some clear features.
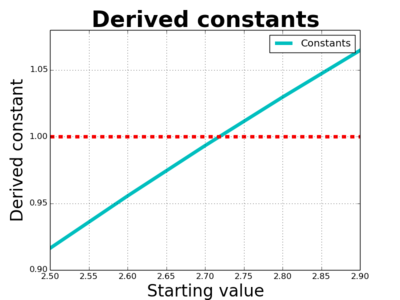
So we can explore this question. Let $x$ be really small, and find a value $S$ such that $\frac{1}{x}(S^x-1)$ is equal to 1. Can we do that? So let's plot between 2.5 and 3.0:
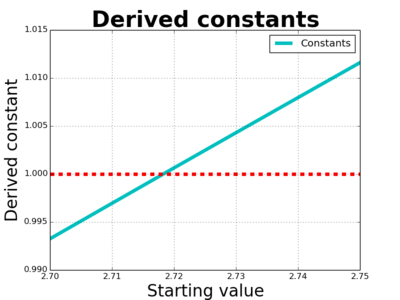
OK, so it's between 2.70 and 2.75 - let's look at that in more detail:
We can now see that it's just a bit less than 2.72 or thereabouts. Some of my readers will have been shouting at the screen for some time now - "It's $e$!! It's $e$!!" Well, yes, it's $e$, also known as Euler's number (Note: not Euler's constant, that's something different). Tracking back through our derivation here, we are trying to solve this problem/question:
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email