
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
2019/01/08 - Elementary estimatesIntroductionEvery now and again as I'm doing various estimates or calculations I use an approximation, and a few days ago it was brought home to me how much I rely on these, and how few people know them. So I thought I'd gather some of them together in one place to be a reference. On the way I've attempted to give broad reasons as to why these are reasonable approximations, but each one can be explored in greater depth, and there are considerable subtleties in places. Even so, I hope these are interesting/useful. By way of setting the scene, if $x$ is small compared to $1$, then $x^2$ is small compared to $x$. As a consequence, if $x$ is very small compared to $1$, $x^2$ is extremely small compared to $1$, and so we can get useful approximations in situations where $x^2$ is negligible. (My thanks to Rob Low[0] for this paragraph).
Getting started ...
So, roughly, when $x$ is small, $(1+x)^2\approx 1 + 2x$. We can see that with a little geometry, as follows.
So the area $(1+x)^2$ is seen to be equal to $1+2x+x^2$. But if $x$ is small enough the contribution of the little blue square is negligible, so we say that the area is roughly $1+2x$ And that's our result. Now taking the square root of each side we can see that when $x$ is small, $\sqrt{1+2x}\approx 1 + x$, which we usually write as $\sqrt{1+x}\approx 1 + x/2$. We'll use these a lot, and that will help you to remember them, but it's definitely worth keeping them close to hand. When $x$ is small:
Another thing to consider is $(1+x)(1-x) = 1-x^2$. When $x$ is small we can again ignore $x^2$, so $(1+x)(1-x) \approx 1$, which means that we have:
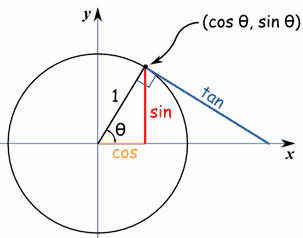
A tad of trig ...Now let's look at distances in a circle. The basic definitions of $\sin(\theta)$, $\cos(\theta)$, and $\tan(\theta)$ are shown.
As the point on the circle moves down towards the $X$-axis you can see that the red line, "sin", gets closer and closer in length to the arc joining the $X$-axis to the point. Thus sin gets closer and closer to $\theta$ (when measured in radians). We can see from the geometry that when $\theta$ is small, $\sin(\theta)$ and $\tan(\theta)$ are very close to $\theta$, and $\cos(\theta)$ is close to $1$. In fact, it's one of my standard mantras that for small $\theta$, $\cos(\theta)$ equals one. This is clearly not true, but in many circumstances it's close enough. Remembering our Pythagoras, we can see from our "obvious" right-angled triangle that $\cos(\theta)^2 + \sin(\theta)^2 = 1$. But as we've said, when $\theta$ is small, $\sin(\theta)\approx\theta$. That means we can rearrange the above to get
So when $\theta$ is small, $\cos(\theta) \approx 1 - \theta^2/2$.
Going a step furtherSince we have now got that $\cos(\theta) \approx 1 - \theta^2/2$, maybe we can extend our approximations a little more so they remain accurate even when $\theta$ or $x$ are a touch bigger. In particular, we observe that $(1+x)^3=1+3x+3x^2+x^3$. Certainly when $x^2$ can be ignored, $x^3$ will be even smaller, so we have:
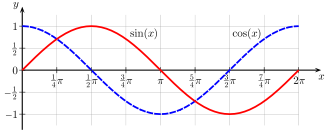
If we look at the graph of $y=\sin(\theta)$, we can see that when $\theta$ is close to zero, the gradient is pretty much 1, which is the value of $\cos(\theta)$, and when $\theta$ is about $\pi/2$, the gradient goes from positive to negative, just as the graph of $\cos(\theta)$ does. We can analyse this further and without too much work (but beyond the purpose and scope of this document) show that the slope (or gradient) of the graph $y = \sin(\theta)$ is the value of $\cos(\theta)$. In other words, $\frac{d}{d\theta}\sin(\theta) = \cos(\theta)$.
Now for the Tangent FunctionTime now to turn our attention to $\tan(\theta)$. When $\theta$ is really small we can see from our diagram that $\tan(\theta)\approx\theta$. We can also see that by recalling that $\tan(\theta)=\sin(\theta)/\cos(\theta)$, and that $\sin(\theta)\approx\theta$ and $\cos(\theta)\approx 1$. But we can go a step further with our more accurate approximations for $\sin$ and $\cos$. Since $\cos(\theta)\approx 1-\theta^2/2$ we also have $1/\cos(\theta)\approx 1+\theta^2/2$. So $\tan(\theta) \approx ( \theta - \theta^3/6 )( 1 + \theta^2/2 )$ which expands to:
SummaryGathering those results together, and remembering that we're assuming that $x$ and $\theta$ are small, we have:
Er, hang on a minute, I think I've noticed something ...
Generalising ...Looking again at the ones on the left in that summary, and re-writing them a bit, we can see a clear pattern:
Another time ...
ReferencesMy thanks to Rob Low on Twitter and other readers for useful comments and feedback.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email