|
OK, so we're going to compute the radius of the Earth by watching
the Sun coming down a building at sunrise. We did this earlier
on the page Latitude Correction, but there's been some question
about the answer, so let's do it "properly".
Let's pick an arbitrary latitude, call it $\lambda$, and we'll
assume that the Earth is a perfect sphere of radius $R$, and that
the Sun's rays are parallel. In effect, the Sun is a point, and
infinitely far away. That means that the line separating light
from dark, the "Terminator" as it's known, is a Great Circle. We
will ignore atmospheric effects. I know that if we actually take
away all the air we'll die, but this is maths, not biology, so
that's OK.
|
You may need to think about that for a bit. |
We'll also assume that we're doing this at Equinox. That means
that the North Pole and the South Pole are both on the Terminator.
The result of this assumption is that we don't need to consider
the tilt of the Earth's axis. If we hover high above the North
Pole we would see the Earth spinning anti-clockwise, the North
Pole lying on the Terminator, and every part of the Earth's
surface spending half its time in light, and half in dark. That
is what "Equinox" means, it comes from Medieval Latin equinoxium,
"equality of night (and day)."
Earth from above
|
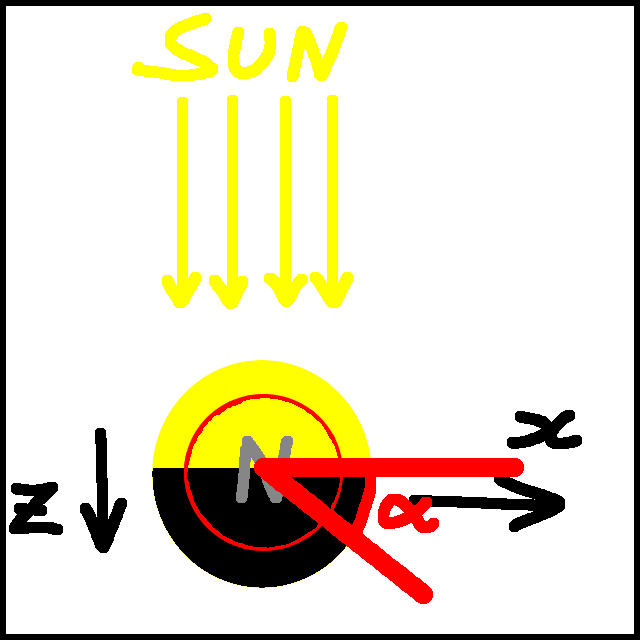
OK, so much for the setup. Here we are, looking down in the Earth
from above the North Pole, the Sun at the top of the image. We
need to define some axes. To some extent this is arbitrary, but
I'm going to take the centre of the Earth as my origin, the Sun
at a very large negative value of $z$, the North Pole at a
positive value of $y$, and $x$ goes off to the right of the
image.
We're also going to have a building at latitude $\lambda$ North,
and its foot will trace out a circle as it goes around. That
has been marked with a red circle on this diagram.
We'll pick up the story at a point when the foot of our building
is still in the dark. That means it is at some angle clockwise
from the $x$-axis. We'll call that angle $\alpha$.
It takes a little work, but we can now compute the $(x,y,z)$
coordinates of the foot of the building. If you're not familiar
with this you can either take the time to check, or just take it
all on faith. I hope at least some of you check ...
The $y$ coordinatate depends only on the latitude, so that's
$R\sin(\lambda)$. The foot of the building sweeps out a circle
of radius $R\cos(\lambda)$, which we'll call $r$. So we have:
- $z=r\sin(\alpha)$
- $x=r\cos(\alpha)$
So summarising, the foot of the building is located at:
- $y=R\sin(\lambda)$
- $z=R\cos(\lambda)\sin(\alpha)$
- $x=R\cos(\lambda)\cos(\alpha)$
OK ... got that?
Now we can immediately get the top of the building, because
that's in the same place, but further from the origin. So the
three-space coordinates of the top of the building are:
- $y=(R+h)\sin(\lambda)$
- $z=(R+h)\cos(\lambda)\sin(\alpha)$
- $x=(R+h)\cos(\lambda)\cos(\alpha)$
That's actually the one we care about, so we'll just use those
coordinates - there should be no risk of confusion.
Earth from behind
|
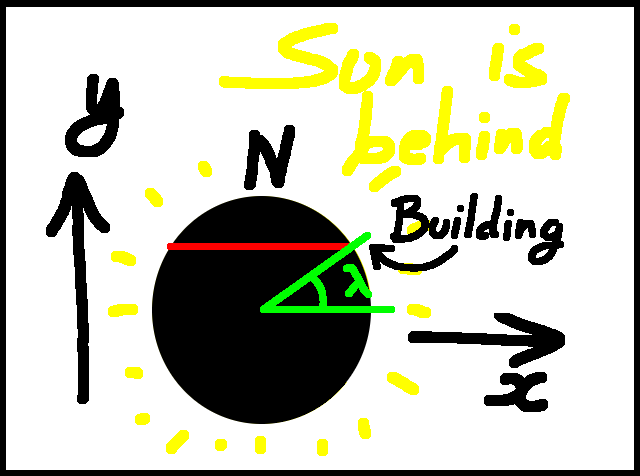
So that's the setup ... what are we actually looking for?
Let's look at the Earth along the $z$-axis, from the shadow. We
see here the situation where the foot of the building has just
arrived at the terminator, illuminated by the Sun from the other
side of the Earth as we look at it from here ... this is when
$\alpha=0$.
So what do we want?
We want, from this point of view, the top of the building to be
on the edge. That means that the coordinates have to satisfy:
Gosh.
So we want this:
- $\left((R+h)\sin(\lambda)\right)^2\;+\;\left((R+h)\cos(\lambda)\cos(\alpha)\right)^2\;=\;R^2$
That simplifies a little:
- $\sin(\lambda)^2\;+\;\cos(\lambda)^2\cos(\alpha)^2\;=\;\left(R/(R+h)\right)^2$
Now $\lambda$ is fixed - that's our latitude. How we proceed
depends on whether we are looking to get the radius from the time,
or the time from the radius. We also remember that $\alpha$ is
small, and $h$ is small compared with $R$. This latter means
that $\frac{R}{R+h}$ is more-or-less $\frac{R-h}{R}$ which is
$1-\frac{h}{R}$.
So let's write:
- $c$ for $\cos(\lambda)$
- $s$ for $\sin(\lambda)$
Now we have:
- $s^2\;+\;c^2\cos(\alpha)^2\;=\;\left(1-\frac{h}{R}\right)^2$
We approximate $\left(1-\frac{h}{R}\right)^2$ by $1-\frac{2h}{R}$
because $h$ is small, and remembering that when $\alpha$ is small,
$\cos(\alpha)\approx{1-\frac{1}{2}\alpha^2}$, so $\cos(\alpha)^2$
comes out as $1-\alpha^2$
Now have:
- $s^2\;+\;c^2(1-\alpha^2)\;=\;1-\frac{2h}{R}$
That's not as bad as it might have been. In fact this is the point
where we observe that $c^2+s^2\;=\;1$. Expanding ...
- $s^2\;+\;c^2(1-\alpha^2)\;=\;1-\frac{2h}{R}$
- $s^2\;+\;c^2\;-\;c^2\alpha^2\;=\;1-\frac{2h}{R}$
- $1\;-\;c^2\alpha^2\;=\;1-\frac{2h}{R}$
- $c^2\alpha^2\;=\;\frac{2h}{R}$
Gosh.
So now we have the fundamental relationship we can do our sums.
Before that, we note that there are 86400 seconds in a day, so
it takes the Earth 86400 seconds to rotate $2\pi$ radians. An
angle $\alpha$ is $\frac{\alpha}{2\pi}$ rotations, so corresponds
to $\frac{\alpha}{2\pi}\times86400$ seconds.
We also note that the Earth's circumference is 40 million metres,
so its radius is about 6.366 million metres.
We'll do the calculations for a latitude of 51.5 degrees, so we
have $\cos(\lambda)\approx0.6225$.
Now read on ...
Radius from time
We start by solving for $R$:
- $R\;=\;\frac{2h}{c^2\alpha^2}$
Let's suppose the building is 5 metres high and we time the sunlight
descending as 28 seconds. What's the size of the Earth?
We need to convert the time to $\alpha$:
- $\alpha\;=\;t\times(2\pi)/86400$
So $\alpha=0.0020362$. Then we get $R$ to be 6.223756 million metres,
which is pretty close.
|
|
Time from radius
We start by making $\alpha$ the subject of our equation:
- $\alpha\;=\;\sqrt{\frac{2h}{c^2R}}$
Then the time for the Sun to descend the
building is roughly:
- $86400\times\frac{1}{2\pi}\sqrt{\frac{2h}{c^2R}}$
where $c^2$ is about 0.3875. So that's about 27.685 seconds.
If the building is four times as high at 20 metres, then the
time will be about twice as long, at about 55.37 seconds.
|
So it turns out that my commenter was absolutely right, and the sums
done on the page Radius Of The Earth Part Two are wrong. The correction
is not as simple as dividing by $\cos(\theta)$, there is more going
on. Now the challenge is to compare the two methods and see where
the other one goes wrong.
That's for another time.
Send us a comment ...
| 



 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email