
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Archimedes' Hat Box Theorem - 2018/05/30
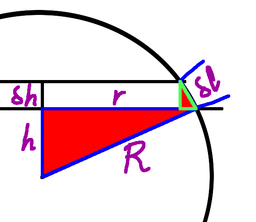
The Archimedes Hat-Box Theorem says these two cylinders have the same surface area. In fact the theorem says that the surface areas are the same no matter how thick the slice is, so as a consequence we can take a "slice" that captures the entire cylinder and sphere, and that means that the surface area of the curved surface of the cylinder is exactly the same as the surface area of the sphere. The cylinder has height $2r$ and circumference $2{\pi}r$, so the area is $4{\pi}r^2.$ But how do we prove this? Suppose the radius of the sphere is $R$, and take a really thin slice. Suppose the base of the slice is at height $h$, and it's of thickness, $\delta{h}$. We can see that the surface area of the slice of cylinder is $2{\pi}R\cdot\delta{h}$. The slice of the sphere is a smaller cylinder with sloping sides. We can see that the radius is smaller, but the slope "adds height" to the cylinder, and we need to allow for that. So if the smaller radius is $r$ and the sloped "height" is $\delta{l}$ then the surface area of the cylinder from the sphere is $2{\pi}r\cdot\delta{l}$ We can see from the diagram that we have similar triangles, marked here in red. Note that the hypotenuse of the little triangle, the one marked $\delta{l}$, is at right angles to the main radius, $R$.
So the surface area of the slopey cylinder is $2{\pi}r\cdot\delta{l}$, which we can bracket as $2{\pi}(r\cdot\delta{l})$. Replacing what's in the brackets we get $2{\pi}(R\cdot\delta{h})$. That is, of course, $2{\pi}R\cdot\delta{h}$, which is the area of the slice through the enclosing cylinder, and we are done. For larger slices we can simply subdivide as finely as we need and get the sum to be as close as necessary to the area of the larger slice. Linearisation is powerful when it works, and it works here. And thus we have Archimedes' Hat Box Theorem.
You might also want to read: Considering A Sphere
Send us a comment ...
|




 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email