 Subscribe! Subscribe!

My latest posts can be
found here:
Previous blog posts:
Additionally, some earlier writings:
|
So on the Doodle Theorem page we have a proof of, yes, you guessed it,
the Doodle Theorem. Here, on a page entitled Another Proof of the Doodle Theorem
we have, yes, you guessed it, another proof of the Doodle Theorem.
The Doodle Theorem says:
|
|
Any map drawn with a single pen stroke that returns
to its starting point can be two-coloured.
|
|
|
Note that you're not allowed to retrace your steps
(as it were), and draw over a line already drawn.
Formally, an Euler Cycle is a list of vertices from the
graph, with repeats, such that the first is the same as
the last (hence "cycle") and such that every edge appears
exactly once. In this way, visiting each vertex in that
order results in a drawing of the graph. |
So a graph that can be drawn with a single pen stroke is,
by construction, planar, connected, and has an Euler Cycle.
The Doodle Theorem is saying that the dual of such a graph is
bi-partite.
It must be admitted that this is not a deep theorem, and of
itself it's not especially important. However, it's a nice
introduction to graph theory, and significantly less well
known than the usual Koenigsberg problem. But there are
several important concepts, and completely accessible.
So here is an alternate proof.
Our opening gambit
We claim the following:
|
|
A graph that can be drawn wth a single pen stroke that
returns to its starting point, can also be drawn without
crossing over a line already drawn.
|
|
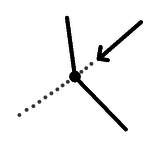
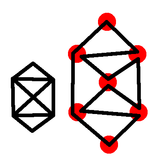
In other words, a planar, connected, Eulerian graph (that is,
has an Euler Cycle) can be drawn such that the situation here
never happens. Here we are part way through drawing our graph,
and we are approaching a vertex, only to find that we have to
cross over a line that already exists.
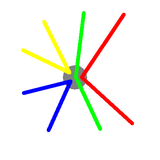
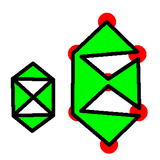
So here's an example of what a vertex has to look like. We've
exploded the vertex to show how the drawing proceeds. It doesn't
matter which colours were drawn first, and it doesn't matter which
direction we were travelling when we drew each colour, what matters
is that they never cross each other during the drawing process.
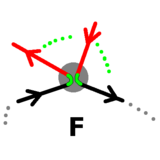
Here is an example of a graph that can be drawn, and we are part
way through an attempt to draw it which will fail. The theorem here
claims that this never need happen.
So how do we prove this? Remarkably, the proof is almost identical
to the usual proof that every graph such that every vertex has even
degree is Eulerian, we just need to carry the extra condition with
us.
Proof
We proceed by induction.
Suppose $G$ is connected, planar, and every vertex has even degree.
Suppose further that every graph satisfying those conditions but
which has fewer edges can be drawn without crossing a previously
drawn line.
Let $F$ be any face in $G$, and remove its edges, giving $G-F$.
Certainly what is left is planar, and at every vertex it either has
its original complement of edges, and so an even number, or two
edges have been removed, so it's still an even number. So each
component of $G-F$ is connected, planar, and has no odd degree
vertices. So by our inductive hypothesis every component of $G-F$
can be drawn as required with no crossing lines.
Now begin drawing $F,$ proceeding clockwise. Whenever we visit a
vertex $v$ in a component of $G-F$ not yet drawn, run around that
(using our inductive hypothesis that we can draw it with no crossing
lines) starting with the edge that is immediately clockwise from
the edge in $F$ just drawn.
|
This require some justification, but a few pictures of
the different cases will soon convince the reader. A complete
and detailed description of all the cases is more work than is
really warranted. |
When we return to $v$ we can continue around $F$ as required. By
continuing around $F$ and ignoring vertices that have already been
drawn we complete the entire traversal of $G$, as required.
It remains only to consider the induction base case(s). Ignoring
the case of the single isolated vertex, the base case is a single
vertex with a single loop, which clearly can be drawn without
crossing any lines.
And so we are done.
Using the new result
Now we can draw our graph, but gently explode each vertex so that
one pair of edges that come in then out as we draw them don't touch
the other edges. Here's an example.
We can see now that our Euler Cycle is basically a distorted
circle - it's a simple closed curve. As such, by the
Jordan Curve Theorem (or in this case simply by common sense) we
can see that it has an inside and an outside.
Colour the inside one colour, and the outside the other colour.
This gives us a bi-colouring of the original planar graph.
Thus we have shown that any connected, planar graph with an
Euler Cycle can be two-coloured. That is, its dual is
bi-partite.
And we're done.
Comments
I've decided no longer to include comments directly via the Disqus
(or any other) system. Instead, I'd be more than delighted to get
emails from people who wish to make comments or engage in discussion.
Comments will then be integrated into the page as and when they are
appropriate.
If the number of emails/comments gets too large to handle then I
might return to a semi-automated system. That's looking increasingly
unlikely.
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email