
Previous posts:
Additionally, here are some earlier writings: |
2021/03/05 - Tesseract TeaserNot the four-dimensional cube sort of Tesseract, this is the Optical Character Recognition (OCR) "Tesseract", software that takes an image of some lettering and produces a plain text file containing the text. Read more: Tesseract Teaser 2021/01/31 - More Mental Model MisstepsI mentioned when talking about an oddity in vim that the behaviour of the command "<n>J" didn't match my mental model. Sometimes software does that, it had behaviour that's totally reasonable when you think about it one way, but there's another way of thinking that causes you to be surprised. Here's another, as reported to me by a friend. Read more: More Mental Model Missteps 2021/01/23 - An Oddity In VIMI'm going to tell you a story, so this is quite a long post. If you'd like to skip the story get directly to the main point then feel free to do so. But if you're interested in the story, make sure you're sitting comfortably, and I'll tell you how I found an oddity in vim. Read more: An Oddity In VIM 2021/01/14 - Double Double Division AlgorithmFor some of my readers, this will all be completely mysterious. But for others, part way through they will go "I recognise this!" So I'd really like to hear from you ... if you recognise this, at which point did the penny drop? I'd also really like to know if you think this is obvious, and possibly even if you've seen it before. Consider the following algorithm. I'll work through an example. I'll divide 450 by 23. Read more: Double Double Division Algorithm
2021/01/01 - Continuity ConcernsRecently, Rachel Wright and I have been watching the episodes of "The Adventures of Paddington Bear" that have been transmitted on broadcast TV here in the UK. It's not exactly gentle viewing, but Paddington is kind, helpful (or tries to be), and it always turns out well. Not very realistic, but if you watch with the right attitude, it is uplifting. Judge us if you will - we don't care. Read more: Continuity Concerns 2020/12/30 - Counting Carbon Calories"When you lose weight, where does it go?" An interesting question, and one where most people haven't thought about it, don't know, and really don't care. But when I was asked, it set in motion a train of thought. Follow along, and see if it makes sense. Read more: Counting Carbon Calories 2020/12/21 - The Parity Of ZeroBefore you react to the title, and before you guess where this is going and form a reaction, pause. I might not be about to say what you expect. Of course, I might, but I might not, and I'd ask you to wait a bit. Read more: The Parity Of Zero 2020/12/12 - When The Text And Html DisagreeSecond Saturday of the month, and that means the Farmers' Market is on. Even in this second lockdown it will be running, with a one-way system and limited numbers permitted inside at any one time. But is it at the usual time? Let's check the email. Oh, I seem to have deleted it. Never mind, there will be a backup ... Read more: When The Text And Html Disagree 2020/10/11 - Recursion Revisited ... a specific exampleSome time ago I wrote a post on Thinking About Recursion, and more recently I wrote about a problem concerning the problem of the number of Vertices Required For Cycles. As it happens, the code for that problem is heavily recursive, and provides a great example of using recursion to solve a real problem. Read more: Recursion Revisited 2020/10/02 - Vertices Required For CyclesBack in late August (the 26th to be precise) Chris Purcell (@ccppurcell@mathstodon.xyz) posted the following:
The first few values are easy enough to compute by hand, but it gets quite tricky quite quickly. How can one construct a (simple undirected) graph with exactly 5 cycles? Read more: Vertices Required For Cycles 2020/08/24 - Reflex ActionsThe machine wouldn't read my credit card. That's not uncommon ... sometimes the contacts on my card are dirty, sometimes the contacts on the machine are dirty ... no big deal. Just lick your thumb, rub the contacts, and try again. Read more: Reflex Actions 2020/07/26 - The Ballad Of BunterIn late May it was becoming increasingly clear that Rachel's laptop was increasingly eccentric. A replacement would be needed, and while it wasn't yet urgent, we felt we should do something before it became so. And so the hunt began. Read more: The Ballad Of Bunter 2020/07/12 - Infinite Ramsey TheoremWith the passing of Ron Graham a few people have been in touch with me to ask what "Ramsey Theory" is. So I've given a brief outline, and pointers in case people want to follow up. In truth, just stick "Ramsey Theory" into your favourite search engine and you'll get lots to follow up and chase down (as opposed, of course, to "follow down" or "chase up"). Read more: Infinite Ramsey Theorem 2020/07/05 - Signal ReflectionWay back in the 70s when I was building logic circuits, I was warned repeatedly that I'd have to get a few things right, or risk "locking up" or "burning out" the CMOS chips I was using. The bogeyman was "Signal Reflection", but no one could tell me what it was, or why it was so bad. Read more: Signal Reflection 2020/07/05 - Analogies Not Considered HarmfulWhile I was writing my post on Signal Reflection, I was given cause to reflect (pun intended ... sorry) on exactly the role and value of analogies in science, maths, and life in general. I've come to the conclusion that, like so many thing, analogies are neither good nor bad. They have their purpose, and each lies somewhere on a spectrum. Read more: Analogies Not Considered Harmful 2020/06/17 - Twitter Reply Vs Quote TweetMore than once now I've seen someone on social media using an option which has, for their purposes, been sub-optimal. In one case it led to a very unpleasant exchange, purely because one person assumed an implication that simply wasn't intended. Read more: Twitter Reply Vs Quote Tweet 2020/06/16 - Proofs To Make You Go WOWFor those of us who love maths, it's sad to see how many people hate it, or have a phobia of it, or proudly announce "I was never very good at maths at school." The question we often counter with is "Would you be so proud of being unable to read?" Read more: Proofs To Make You Go WOW 2020/06/08 - Laptop Purchase Advice ReceivedRachel's laptop has become ... eccentric. Like a toddler, or an aging relative, who won't get up in the morning, won't go to bed at night, and won't play nicely with others, I'm afraid The Admirable Crichton has taken to not starting up properly, not shutting down properly, and occasionally just refusing to connect either over ethernet, or Wi-Fi. Read more: Laptop Purchase Advice Received 2020/05/29 - Blow Up Your Ability BalloonIt's pretty clear to most of us that skills unpractised are eventually lost. Anything at the limits of our abilities need to be exercised regularly to avoid having them waste away. Read more: Blow Up Your Ability Balloon 2020/05/27 - A Factlet For AllMore and more often I hear people saying and see people writing "factoid", by which they mean "A Small Fact". But is that right? Read more: A Factlet For All 2020/05/22 - Anatomy Of A HitRecently I found something I wrote a while ago, and with one or two touches I thought it was worth recycling. So I refreshed it a little and integrated it into my blog. As is my wont I then mentioned it in a couple of places, and went back to work. Imagine my surprise when it suddenly got a lot of attention. Indeed, I was very surprised, and I set up some tracking to see what happened ... this is the report. Read more: Anatomy Of A Hit 2020/05/20 - Sell Yourself Sell Your WorkDoing technically brilliant work may be enough for your personal gratification, but you should never think it's enough. If you lock yourself in a room and do the most marvellous work but don't tell anyone, then no one will know, no one will benefit, and the work will be lost. You may as well not have bothered. For the world to benefit from your work, and therefore for you to benefit fully from your work, you have to make it known. Read more: Sell Yourself Sell Your Work 2020/05/18 - All The LettersMost people are aware of the phrase:
2020/05/09 - Being Slow To Criticise
This post is not about that story. This post is about a comment made by one of the readers in the forum where I saw it. Read more: Being Slow To Criticise 2020/05/01 - State Machine In Real Life
Read more: State Machine In Real Life 2020/04/27 - Coxeter Once Nerd Sniped Conway
So here is the story, as told to me by Conway at MathFest, 2015 ... Read more: Coxeter Once Nerd Sniped Conway 2020/04/21 - Not Always Your Fault"I must have done something wrong." Read more: Not Always Your Fault 2020/04/12 - Remembering ConwayThis is impossible to write. I'll try anyway. John Conway has left us. Read more: Remembering Conway 2020/04/03 - Perception Of SpaceDuring this time of lockdown and/or self-isolation, it's tempting for those of us content with our own company to sit tight indoors and wait it out. But I'm reminding of some stories told to me by my friend Laurie Brokenshire. Read more: Perception Of Space 2020/03/21 - Parallelogram PuzzleA while ago (March 2nd at 16:28 to be reasonably precise) Ed Southall asked a great question on Twitter: Read more: Parallelogram Puzzle 2020/03/12 - Back Of The Envelope COVID19I did a rough "Back of the Envelope" calculation about COVID-19. Read more: Back Of The Envelope COVID19 2020/03/09 - A Point Against The Axiom Of Choice
In this post we look at one of the implications of accepting the Axiom Of Choice, and wonder if it's so obvious after all. Read more: A Point Against The Axiom Of Choice 2020/02/26 - In Defense Of The Axiom Of Choice
Read more: In Defense Of The Axiom Of Choice 2020/02/21 - Journeying Home Through Storm Dennis
Read more: Journeying Home Through Storm Dennis 2020/02/09 - Earth Radius Refined
Read more: Earth Radius Refined 2020/01/05 - Volume Of A Sphere
Click here to see the original Then there was an image with the actual formula: $V=\frac{4}{3}{\pi}r^3$. Over 12 thousand people "Liked" the tweet, but someone said:
Read more: Volume Of A Sphere 2019/12/04 - Big Oh And RelationsIn an earlier post we saw that $f(n)=n$ dominates $g(n)=n-\ln(n)$, but that's no surprise. What does come as a surprise is that $g$ dominates $f$. So even though for any value of $n$ greater than $2$ we already have $f(n)>g(n)$, still we say that $g$ dominates $f$. That feels very unexpected, and as a result you might question the value of the concept of "dominates", so let's pause and take a moment to get a handle on what's going on. Read more: Big Oh And Relations 2019/11/19 - Mathematical RelationsUbiquitous in mathematics is the concept of comparing things, and examining the relationships between them. Since we do that all the time and everywhere, it's worth having a look at the concept of a "Relation" in an abstract sense to try to tease out the common themes. Read more: Mathematical Relations 2019/10/24 - Introducing Big OhLast time I said:
This post is going to look at that carefully. Algorithms can behave erratically, so the concept of "this looks like that" isn't really enough, we would like to do better. Read more: Introducing Big Oh 2019/10/11 - Constant DifferencesSo we've seen what a "Problem" is, what an "Instance" is, and talked a little about the "Size" of an instance, and what an "Algorithm" is. Now it's time to look more closely at what we mean when we talk about the time an algorithm takes, and some implications thereof. Read more: Constant Differences 2019/10/05 - Algorithms And Sizes Of InstancesIn the last post, Introducing Time Complexity, we look at what we mean by a "Problem", and by an "Instance" of a problem. Now we'll start to think about Algorithms, and meet the idea of how long an algorithm takes. Read more: Algorithms And Sizes Of Instances 2019/09/30 - Introducing Time ComplexityA short time ago I was chatting about and working on some puzzles with a friend, and I casually mentioned something about how the time complexity of this particular problem behaved. What then transpired was that my friend didn't know anything about how the whole "Time Complexity" thing worked, and didn't understand about $P$ versus $NP$ and similar concepts. Read more: Introducing Time Complexity 2019/09/14 - The Linear FrogI was given a problem recently, and I was really pleased to get the solution. I wonder if you can (a) solve it, and (b) tell me where it comes from. I've not been able to track it down at all. Read more: The Linear Frog 2019/08/24 - Seventy Versus One Hundred RevisitedIn Seventy Versus One Hundred we looked at the situation of two identical cars, one doing 70, the other doing 100, slamming on their brakes at exactly the same location to avoid an obstruction. The slower car stops in time, the faster doesn't, and the question was to compute the speed at impact. The model we used there was that the two cars shed the same amount of energy in the distance they have, so we're assuming that energy is shed at a rate proportional to the distance travelled. But maybe the rate energy is shed is proportional to time, and not distance. What happens then? Read more: Seventy Versus One Hundred Revisited 2019/08/17 - How The Farrago WorksSome time ago I was asked about the way this website works, and as I started to explain, I realised just how much there was going on and how complicated it seemed. But they seemed to think it was neat and elegant, so I thought I'd write it up. Read more: How The Farrago Works 2019/08/05 - Seventy Versus One HundredSupposed two identical cars are traveling along the same straight road, with one traveling at 70 kilometres an hour, the other at 100 kilometres an hour. Just as the faster car draws roughly level with the slower, they both see an obstruction in the road ahead, and (as luck would have it) at the exact same moment, exactly when they are level with each other, they both slam on the brakes. Read more: Seventy Versus One Hundred 2019/07/22 - Powers Of Two In Lex OrderRecently I was sent a lovely little twitchet, so I thought I'd share it for people to think about. No answers provided ... Read more: Powers Of Two In Lex Order 2019/07/16 - Emerging E ExpandedAs an experiment, we can punch "10" into a calculator and take the square root. Given that we're starting with a number that's bigger than 1, it's no real surprise that we get a smaller number. In fact, we get 3.16227766... We can take the square root of that, and we get 1.77827941... Now, if you actively like numbers, you may think that that is quite close to one and seven ninths, or $1\frac{7}{9}$. If we write that as an "improper fraction" it's $16/9$. And the fun thing about $16/9$ is that both $16$ and $9$ are squares, so if we take the square root again we should get something very close to $4/3$. Read more: Emerging E Expanded 2019/07/13 - Rage Inducing System ImplementationI'm about to go on an extended business trip, so I'm making note of broadcast TV programs that I want to record, and making sure there is enough space on the recorder. I have a large external HDD attached, so I've been transferring programs to that to make space on the internal HDD. All was going well. There's still 240 hours of space on the external HDD, so no problems anticipated. Read more: Rage Inducing System Implementation 2019/06/19 - The Book Is Not Always RightRecently someone tweeted a picture of a page from a book. It seems to be some sort a book about maths aimed at students, but in one simple paragraph there was just so much wrong, it attracted many comments from many of my friends and colleagues. Read more: The Book Is Not Always Right 2019/06/13 - Emerging EStart with 10, and square root many times over. After a while you get 1+(rubbish). Taking the square root of that halves the rubbish, so we can deduce that $10^\epsilon = 1+c_{10}\epsilon$. I've put the subscript on the $c$ because if you do this again but start with 5 instead of 10 you get a different constant, $c_5$. So now we have a function, $c(x)$ where you start with $x$, successively square root, compute the constant, and that's the value of the function. If we do this there are lots of questions to ask about the function $c$. Read more: Emerging E 2019/06/09 - Impossible To TranslateSome time ago while on a business trip to Spain I was asked a question that turns out to be impossible to translate. Read more: Impossible To Translate 2019/05/29 - Waiting In VainOver the past few years I've occasionally been contacted by my ISP[0] to say that one of my scripts had gone rogue and was using 100% CPU, and would it be OK to kill it. This has always been a surprise to me because I'm usually pretty careful about my code, especially when it's running "out there" on someone else's hardware. Read more: Waiting In Vain 2019/05/24 - Non Repeating DecimalsIn the previous post we talked about repeating decimals, and showed that every (eventually) repeating decimal is a rational number, and that every rational number has a (possibly trivial) (eventually) repeating decimal representation. Now we'll look at some cases of decimals that don't repeat, and hence are irrational. Read more: Non Repeating Decimals 2019/05/09 - Rational RepeatsRecently on-line I saw someone talking about the decimal expansion of pi, and they said: "I'm told pi goes on forever and never repeats, I can't see how that can be proved." Read more: Rational Repeats 2019/05/05 - Why Is It LovelyRecently on one of my "social network feeds" I saw a post saying:
Read more: Why Is It Lovely 2019/04/30 - Compiling Crypto ConnectionsHaving given the maths club talk last Saturday (which went very well) I was left with the preparative work that I'd done. That consists of lists of concepts, people, algorithms, cryptosystems, and some of the connections between them. Read more: Compiling Crypto Connections 2019/04/20 - Exploring Connections Between Crypto SystemsI'm giving a talk for the Liverpool Maths Club this Saturday, April 23rd, 2019. I do this roughly twice a year, and it's always a real challenge - the ages range between 13 and 18, and while some of the students have been coming for years, for others it might be their first time. So whatever the topic might be, it needs to be engaging, accessible, and challenging, all at the same time. Read more: Exploring Connections Between Crypto Systems 2019/04/13 - Elwyn Berlekamp Has Left UsI remember meeting Elwyn Berlekamp. Read more: Elwyn Berlekamp Has Left Us 2019/04/07 - Root Cause Analysis And The Photocopier Question"Root Cause Analysis" is complex, involved, and requires both tenacity and creativity. When there's a problem, often the cause isn't a simple, single thing, it's often a collection of things, and each of those might not be easily characterised. Even so, it's a crucial exercise in many technology based industries and activities. So in this post I want to talk about my most recent brush with the challenges of performing RCA, and even of getting other people to see that it's there to be done. Read more: Root Cause Analysis And The Photocopier Question 2019/03/28 - The Up Down TidesSo while in orbit at about the altitude of the ISS we've looked at throwing a ball sideways, and we've looked at throwing a ball forwards or backwards. What happens if we throw the ball up? Or down? Is that different? Do we finally have the ball travel away in a straight line at a constant speed? What new horrors lie in store? Read more: The Up Down Tides 2019/03/18 - The Fore Aft TideIn our last post we saw that when we're in orbit, if we throw a ball very gently in exactly the right direction, somehow it bounces back and forth through our position. We experience a fictitious force, pulling the ball back to a resting position, so it moves in Simple Harmonic Motion. So remember the setup. You're in orbit around the Earth with the International Space Station, and you have a juggling ball. You hold it next to your helmet and release it, and it just stays there, apparently floating. Now gently push the ball ahead of you in orbit. In effect you are throwing the ball away from you. What happens this time? Well, it depends. Read more: The Fore Aft Tide 2019/03/12 - The Sideways TideStand outside the International Space Station and hold a juggling ball right by your helmet. Let it go, and it will stay there. Apparently this is incredibly difficult to do because you always move slightly as you let it go and withdraw your hand, but in theory, it will just hang there, because you are in weightless conditions. Now give it a gentle push "sideways". As you will probably know, it will then travel away from you in a straight line at a constant speed, because that's what happens in zero gravity. But it doesn't ... Read more: The Sideways Tide 2019/03/05 - Wrapping Up Wrapping Up The EarthWe're coming to the end of this series. Our friend has purchased too much rope, too little rope, too much miraculous wrapping sheet, and now, finally, we come to the question of too little. But first, let's look at the different "rope" scenarios, and see what happens in each of the analogous "sheet" cases. Read more: Wrapping Up Wrapping Up The Earth 2019/02/26 - The Other Wrapping The Earth ProblemHaving gone around the world to wrap it, in truth our friend is too tired (or too lazy) to prop up the wrapping everywhere. So just as in The Other Rope Around The Earth problem, instead we look at propping it up in just one place. We need to take up one million square metres of excess. How high will that tent pole have to be? Read more: The Other Wrapping The Earth Problem 2019/02/19 - Wrapping The EarthOur friend once again has too much to drink, and once again indulges in a little late night internet shopping. This time, however, it's fueled by curiousity, having discovered that there is a material that is infinitely stretchy, but which always retains its area. So while you can stretch it one direction, it will keep its area by shrinking in another direction. Read more: Wrapping The Earth 2019/02/12 - The Ring Of SteelOur friend has encircled the Earth with Rope, discovered that it's 6 metres longer than needed, so expanded the circle by 0.95 metres to take up the slack. Thus we have a ring of rope around the Earth at height just about 1 metre. But overnight, somehow, magically, the rope gets converted to steel! Then, over breakfast, a slight Earth tremor gently rattles the props, and they all fall down, leaving the ring of steel completely unsupported. What happens next? Read more: The Ring Of Steel 2019/02/05 - Rounding Up The RopesWe've seen the $(Other)^k$ rope around the Earth for $k=0, 1, 2,$ and $3$. In this post we'll look at $k=4$, but we'll start with a "heads up" for where we'll go next. Read more: Rounding Up The Ropes 2019/01/29 - The $(Other)^3$ Rope Around the EarthSo we have:
Read more: The Other Other Other Rope Around The Earth 2019/01/21 - Rope Around The Earth RefinedAs previously mentioned, the Rope Around the Earth problem is a lovely one, and everyone should know it. But even if you do, there's still a nice added extra. In this post we'll have a look at that. Read more: Rope Around The Earth Refined 2019/01/15 - The Other Rope Around The EarthThe well-known "Rope Around the Earth" problem is lovely, and, as I say, well known. But some time ago David Bedford mentioned another rope around the Earth problem. A different rope around the Earth problem. And it goes like this. Read more: The Other Rope Around The Earth 2019/01/08 - Elementary EstimatesEvery now and again as I'm doing various estimates or calculations I use an approximation, and a few days ago it was brought home to me how much I rely on these, and how few people know them. So I thought I'd gather some of them together in one place to be a reference. Read more: Elementary Estimates 2019/01/01 - Latitude CorrectionRecently I've been discussing the details of measuring the size of the Earth by watching a shadow descending a wall at sunrise, or ascending at sunset. The sums are easy enough if you do it at either Equinox, and at the Equator. But what if you're not at the Equator? What then? Read more: Latitude Correction 2018/10/07 - Just Give Me The AnswerA while ago I saw an exchange on a programming forum I visit on occasion. A poster had asked a question that at first sight (and in all honesty, subsequent examination) appeared pretty simple. The poster claimed to have tried everything they could think of, that nothing worked, and they'd appreciate any help. Read more: Just Give Me The Answer 2018/09/19 - More Musing On Pollard RhoAfter my previous post I started to explore a little more about how the function in Pollard Rho affects what's going on. As yet I've not come to any conclusions, and I'm currently deep in the "I'm confused" stage of the exploration. I'm sure there are other people know all this, but I don't know who they are, and haven't been able to find any write-ups, so I'll just carry on. Read more: More Musing On Pollard Rho 2018/09/10 - Idle Thoughts About Pollard Rho
Read more: Idle Thoughts About Pollard Rho 2018/09/04 - When Optimising Code MeasureThis is a truism that lots of people quote, but it can be hard to remember, especially in the heat of battle (as it were). Rather fortunately it came to mind just when needed, as I found something completely unexpected. Read more: When Optimising Code Measure 2018/08/27 - A Dog Called MixtureSome considerable time ago I was giving some talks at a school, and my wife and I were kindly hosted at the home of the Headmaster and his family. And his menagerie, as it turned out. Read more: A Dog Called Mixture 2018/08/03 - Another Pay Pal ScamReceived as part of the newsletter of a publishing company ... We've been living in interesting times at Wildside Press since our last newsletter. Our PayPal account was VERY creatively hacked, and we briefly lost about $15,000 of the money we'd been saving up for royalty payments to authors. Read more: Another Pay Pal Scam 2018/06/13 - Why Top Posting Has WonI've recently realised that, in my head, there's a connection between top-posting in email and washing the dishes. Stay with me, I'll see if I can make the connection for you. Read more: Why Top Posting Has Won 2018/06/07 - Unexpected Interaction Of FeaturesI've been dealing with some data, and using my usual technique of using command-line tools to play with it for a while before writing a program to do the full analysis. But something was wrong, and it took me a while to work it out. Read more: Unexpected Interaction Of Features 2018/05/30 - Archimedes Hat Box Theorem
The Archimedes Hat-Box Theorem says these two cylinders have the same surface area. In fact the theorem says that the surface areas are the same no matter how thick the slice is, so as a consequence we can take a "slice" that captures the entire cylinder and sphere, and that means that the surface area of the curved surface of the cylinder is exactly the same as the surface area of the sphere. Read more: Archimedes Hat Box Theorem 2018/05/29 - Considering A Sphere
Someone else then asked if there was a similar visualisation of the volume of a sphere, or the surface area of a sphere, and that started me thinking ... Read more: Considering A Sphere 2018/05/17 - To Link Or Not To LinkOver the past few years I've noticed a rise in a particular type of spam that I'm receiving. It takes the form of an email like this: Read more: To Link Or Not To Link 2018/05/07 - Generic Advice For Writing A ThesisI have some generic thesis-writing advice to supplement that given by your supervisor, but only if it's welcome. Read more: Generic Advice For Writing A Thesis 2018/02/18 - Just Teach My Child The Maths
Read more: Just Teach My Child The Maths 2017/12/13 - Not A Spectator SportOne of my university lecturers gave what we all thought were dreadful lectures. Muddled, unclear, chaotic, with no discernible thread. It took ages to reconstruct and rework the material to a point where we could attack the problems and old exam questions. Read more: Not A Spectator Sport 2017/10/21 - Left Truncatable PrimeRecently Maths Inspiration produced some pencils with a fantastic idea. Yes, their name is on it, yes, it has a slightly cheesy catch-phrase, But then there is something really clever. Read more: Left Truncatable Prime 2017/10/15 - The Doctor And The LawyerA doctor and a lawyer were chatting at a party when someone approached the doctor. They wanted advice, and started to describe their symptoms when the doctor interrupted. "It might be better," he suggested, "to make an appointment so we can talk in private." Read more: The Doctor And The Lawyer 2017/10/03 - Four Points Two Distances ProofThe Four Points Puzzle challenge that Peter Winkler set me was this:
It's the proof that matters. Here's mine. Read more: Four Points Two Distances Proof 2017/10/01 - Meeting Ron GrahamI was a lowly PhD student when I first met Ron Graham. It was at a conference, and there was something I wanted to show him. In my mind it was pretty much guaranteed that he would be interested, but he was (and still is!) extremely well known, extremely eminent, and extremely popular. As a result he is extremely busy, and somewhat besieged with people, all wanting a piece of his time. How could I possibly attract and hold his attention long enough to get him interested? So I hatched a plan. Read more: Meeting Ron Graham 2017/09/28 - Napkin Ring Versus Spherical CapMany years ago I was at a semi-social gathering and a somewhat odd incident occurred. Over the course of conversation it emerged that I was studying maths, and one chap, at one point, turned to me and said: "So, do you like puzzles, then?" Read more: Napkin Ring Versus Spherical Cap 2017/09/26 - The Four Points PuzzleAt the MOVES conference in New York in August I was lucky enough to spend some time with Peter Winkler, mathematician, puzzle master extraordinaire, and author of "Mathematical Puzzles: A Connoisseur's Collection". As we talked about many things he set me this puzzle:
Read more: The Four Points Puzzle 2017/09/16 - Radius Of The Earth Part TwoSome nine and a bit weeks ago I posted about a method of calculating (or estimating) The Radius Of The Earth using a stopwatch and watching the Sun at sunrise (or sunset). When "Mike the Sundial" told me the idea I was just stunned at the simplicity and elegance. Colin Beveridge took up the challenge, and you can read his account of his method here: When I read that I was interested to see just how different his take was from mine. Read more: Radius Of The Earth Part Two 2017/07/28 - Grep Timing AnomalySome considerable time ago - long enough that probably the details are no longer relevant, or accurate - I got seriously fed up with the spam filtering on my email service. There were so many false positives that I had to wade through the spam bin every day, pulling out obviously good emails that needed attention. It got so that it cost me more time to have it running. Read more: Grep Timing Anomaly 2017/07/12 - The Radius Of The EarthThe talk/workshop I give about computing the distance to the Moon uses, it claims, nothing more than a pendulum and a stopwatch. And while it's sort of true that it uses nothing else, it's not really true, because it also uses the period of the Moon, and the size of the Earth. Now it might be possible to persuade you that it's OK to use the period of the Moon, since you can simply look out the window and measure that for yourself, but to use the size of the Earth seems a bit of a stretch. Surely there's no way to compute that from your back garden. Read more: The Radius Of The Earth 2017/07/09 - This Works To Cure My HiccoughsIt's many years ago that I was told about this trick. People rarely believe me, but it honestly works for me, and it has worked for others. So I thought I'd write it up. Read more: This Works To Cure My Hiccoughs 2017/07/02 - Perhaps We Saved OneMany years ago a good friend of mine, Bill Mullarkey, organised a "Science and Technology Extravaganza" in Wigan. It was a fabulous two-day event with hundreds of teenagers and adults in attendance. The buzz of excitement was huge, and it was an honour to be part of the whole thing. Read more: Perhaps We Saved One 2017/06/18 - Thinking About MastodonSome people are describing Mastodon as a decentralised Twitter, but that's rather misleading. It's better not to try to understand it like that. Read more: Thinking About Mastodon 2017/06/17 - Disappearing Trains On VirginThis is part of the series on Virgin Train Ticket Search Oddities Read more: Disappearing Trains On Virgin 2017/04/16 - The Independence GameA few weeks ago I was honoured to be able to attend the gathering at the Royal Society where Rob Eastaway was given his Christopher Zeeman medal. He gave an excellent talk, full of interest and humour, the only downside being that he made us play a game. I don't remember if he gave it a name (Update: Rob calls it "Avoid the Neighbours") but I now think of it simply as "Rob's Dots". He said he didn't know how to play it optimally beyond 11 points, so I thought I'd have a go. Read more: The Independence Game 2017/04/03 - One Of My Favourite PuzzlesIt is impossible to choose a single problem as my favourite. There are so many, each with their own attractions, each with their own charms. But there is one that I solved quickly, and then found that I had only just started to scratch the surface. Read more: One Of My Favourite Puzzles 2017/03/08 - Thinking About RecursionIt has been said that there are two hard problems in computing:
Read more: Thinking About Recursion 2016/12/03 - Memorising The TubeRecently I memorised the periodic table of elements. When I tell people that, the response has generally been a moderate pause, followed by a rather puzzled - "Why?" So I thought I'd explain. Read more: Memorising The Tube 2016/11/19 - Spikey SpheresI've recently been working on an optimisation problem, and I've come to realise that I can consider it as wandering around on a smooth landscape in 1800 dimensions. The problem is that while the error function may be "smooth," your intuition of what this means is wrong. Read more: Spikey Spheres 2016/10/06 - Surprisingly QuickIn the 1990s I had a job at Liverpool University doing research into how we might make it possible for non-computing specialists to use parallel computers. Even today, over 20 years later, this is still an unsolved problem, and the machines now are designed to be easier to use. The machine I was using was a Parsys SuperNode with 96 T800 transputers, hooked together with a reconfigurable switch, cunningly designed so that any 4-regular network could be realised. Read more: Surprisingly Quick 2016/09/18 - An Unexpected FractionOn 2016-09-09, @MEIMaths tweeted an image and said:
From the way it's phrased you'd expect the answer to be the same regardless of the quadrilateral chosen ... Read more: An Unexpected Fraction 2016/08/28 - You Have To Admire Their OptimismComing back from Australia, Rachel Wright and I landed at Heathrow (which we usually avoid) and caught trains back home. Our final leg was from Chester to home, and I had a look at the live departures board to see how things were looking. Read more: You Have To Admire Their Optimism 2016/07/10 - Representatives MatterMy uncle has a Ferrari, and it has led him to make an interesting observation. Read more: Representatives Matter 2016/06/08 - Pythagoras By IncircleSome time ago I was working on a puzzle about incircles, and unexpectedly a proof of Pythagoras' Theorem dropped out! I'm sure it's well known to people who know lots about Pythagoras' Theorem, but I thought I'd share it. Read more: Pythagoras By Incircle 2016/05/31 - A Puzzle About PuzzlesSome time ago a friend of mine, Adam Atkinson, mentioned to me what he referred to as "Semi-Chestnuts" - puzzles that should be classics, but are for some reason effectively unknown. Recently one of these caught the attention of the Twitter-verse. Read more: A Puzzle About Puzzles 2016/05/24 - How Not To Do TwitterRecently I had an exchange on Twitter that beautifully exemplifies how companies get it so totally, totally wrong. Usually I don't name names, but on this occasion it's just spectacularly bad, and then they asked me to point them at a write-up, that I've decided to go ahead and do so. Read more: How Not To Do Twitter 2016/01/04 - Calculating 52 Factorial By HandSome time ago I gave a talk where I showed that something unexpected happening with a deck of playing cards. I had some volunteers try it, and while they did so I talked about just how many orderings there are for 52 cards. To do this I computed (an approximation to) $52!$ (52 factorial) by hand. It's not so hard - you just calculate $54!$ and then divide by 3000. Read more: Calculating 52 Factorial By Hand 2016/01/02 - Small Things Might Not Be So SmallTwenty years ago (or thereabouts) there was a Christmas road safety campaign in which they said: "Wearing a seatbelt doubles your chance of surviving an accident." But that's obviously nonsense. Read more: Small Things Might Not Be So Small 2015/12/20 - Not If You HurryOn one occasion, when I was a teenager, I was in the car with my parents going somewhere. We had to turn right (equivalent to turning left in the States) and hence had to cross a lane of traffic and merge into the far lane. My father was looking to the right to see if there was anything approaching in the lane we had to cross, and asked my mother - "Is there anything coming?" Read more: Not If You Hurry 2015/12/17 - Factoring Via Graph Three ColouringOccasionally someone comes to me and says that they have a polynomial time algorithm for solving an NP-Complete problem. More specifically, someone came to me and said they could Graph Vertex Three Colour (G3C) in polynomial time. They'd tried lots of example, and it always worked. So I produced a graph ... they never came back. Read more: Factoring Via Graph Three Colouring 2015/12/16 - Another Proof Of The Doodle TheoremSo on the Doodle Theorem page we have a proof of, yes, you guessed it, the Doodle Theorem. Here, on a page entitled Another Proof of the Doodle Theorem we have, yes, you guessed it, another proof of the Doodle Theorem. Read more: Another Proof Of The Doodle Theorem 2015/12/15 - When Obvious Is Not ObviousThere's an old story that goes something like this: A math professor is teaching a class, and in the middle of a proof he says "Clearly we have the following." A student puts up his hand and says: "That's not clear to me." Read more: When Obvious Is Not Obvious 2015/12/13 - Graph Three Colouring
Read more: Graph Three Colouring 2015/12/12 - The Doodle TheoremThe Doodle Theorem says:
Read more: The Doodle Theorem 2015/10/25 - Be Careful What You SayHere's an amazing story. A young child writing to a popular television programme with wild claims and, quite frankly, ridiculous aspirations. The output is a lesson to us all. Read more: Be Careful What You Say 2015/10/10 - The Mutilated Chessboard RevisitedPuzzle enthusiasts know that a really good puzzle is more than just a problem to solve. The very best problems and puzzles can provide insights that go beyond the original setting. Sometimes even classic puzzles can turn up something new and interesting. Read more: The Mutilated Chessboard Revisited 2015/08/16 - A Mirror CopiedSo earlier I asked: What do you get when you photocopy a mirror? But the real question, as I then expanded, is not "What do you get?" but: "Why must you get that?" Can we deduce from first principles, based only on what a good photocopier must do, what the result will be? I claim the answer is "Yes," although there are some who disagree. Read more: A Mirror Copied 2015/08/01 - The Other Other Rope Around The Earth
There's a classic problem: Read more: The Other Other Rope Around The Earth 2015/07/29 - Photocopy A MirrorRecently on Twitter I asked the question:
2015/06/06 - The Point Of The Banach Tarski TheoremThere's a classic "Limited Audience" joke/riddle that goes:
Read more: The Point Of The Banach Tarski Theorem 2015/05/24 - Sieve Of Eratosthenes In Python
Read more: Sieve Of Eratosthenes In Python 2015/05/19 - Fast Perrin TestSo we've got scaffolding to look for Perrin Pseudo-Primes (PPPs), assuming any exist (which they do) but as we run the existing code we find that it's spending pretty much all its time in the test as to whether n divides k(n). Now we look to speed that up ... Read more: Fast Perrin Test 2015/05/18 - Russian Peasant MultiplicationSometimes simply called "Peasant Multiplication," sometimes called "Ancient Egyptian multiplication," sometimes called "Ethiopian multiplication," sometimes called "Multiplication by Doubling and Halving," this algorithm is well-known to some, a mystery to others, and more useful than you might think, being applicable not just to multiplication of numbers, but also useful for exponentiation, and for matrices. Read more: Russian Peasant Multiplication 2015/05/17 - FindingPerrinPseudoPrimes Part2So now we've got the scaffolding of a program to find these Perrin Pseudo-Primes. Here is the main loop of the code, with some simplistic timing added to it. (Note that this code is incomplete and won't run as is). The output shows that when given 100 seconds to run it gets as far as n=42763, but more importantly, the timing shows that it overwhelmingly spends all of its time in the routine to test whether or not a number passes the "Perrin Test." So there are a few things we need to do. Read more: FindingPerrinPseudoPrimes Part2 2015/05/15 - FindingPerrinPseudoPrimes Part1Some 20 years ago I was chatting with a friend of mine, and he said something like the following: Read more: FindingPerrinPseudoPrimes Part1 2015/05/13 - The Unwise Update
Read more: The Unwise Update 2015/05/03 - Miles Per GallonI remember a while ago attending a talk that did something utterly bizarre with units of "miles per gallon." I don't remember much about it, but I thought I'd attempt to reconstruct the process in a post, just to see how far I get, what conclusion I reach, and whether people think it's as bonkers as I do. Here we go ... Read more: Miles Per Gallon 2015/05/02 - Tracking An Item On Hacker NewsA couple of weeks ago I had an exchange with a user on Hacker News about user "ages." I wrote that up in my previous post, and then submitted it. I was surprised that the item garnered enough attention to make it to the front page, but that was when a little foresight paid off. I don't usually bother with analytics on my site, but on this occasion I put a tracker on the page to count the number and times of page hits. Read more: Tracking An Item On Hacker News 2015/04/19 - Hacker News User AgesA few days ago I was reading Hacker News[0] and someone had posted a poll[1] with the following question: Read more: Hacker News User Ages 2015/04/14 - Poking The Dusty CornersIn chatting with people about what a maths degree is, and what it does for you, I've often been intrigued by a particular response. I've shown them something that they expect to be true (or false) and then shown that their expectations can be confounded. When I do that, a common response is "Well, you're just being stupid." Read more: Poking The Dusty Corners 2015/04/03 - There Is No Time For This
Read more: There Is No Time For This 2015/01/05 - Publically Sharing Links
Read more: Publically Sharing Links 2014/12/14 - Learning Times TablesShould primary school students be drilled on their times tables? Read more: Learning Times Tables 2014/12/12 - Graceful DegradationI first learned about graceful degradation from a colleague. He prefaced his story by saying that good people learn from their mistakes, but the best people learn from other people's mistakes. This is a bit like the saying in aviation circles that a good landing is one you can walk away from, an excellent landing is when they can use the 'plane again ... Read more: Graceful Degradation 2014/11/22 - Diagramming Maths TopicsAn impossible task, but wouldn't it be useful to have some sort of diagram of topics in maths, connected somehow to show the links between topics? How could such a diagram been created? How could it be explored? How could it be dynamic? Maintainable? Usable? Read more: Diagramming Maths Topics 2014/08/26 On The RackWhen travelling, I usually go as light as possible. Certainly when travelling by plane I try to go "hand luggage only", and when doing various mini-tours of talks, etc., I try to travel with just a single, small backpack. Sometimes it's not possible, but I usually manage. Here's a story of one time when this had unexpected consequences ... Read more: On The Rack 2014/08/11 Square Root By Long DivisionThe other day someone asked:
Read more: Square Root By Long Division 2014/05/23 Beyond The BoundaryIn which we show that 1+2+4+8+16+... is not equal to -1, and how that might both surprise us, and not surprise us. Read more: Beyond The Boundary 2014/05/03 Fill In The GapsRecently I had an interesting conversation on twitter, insofar as one can have a conversation at all in that medium. It started with the following perfectly reasonable question ...
Q> Sorry for what may be a stupid question, Q> but sin(x)/x has a limit of 1 as x -> 0, Q> so does it not cross x=0 at 1? Read more: Fill In The Gaps 2014/04/24 Software ChecklistDuring the second World War, fighter pilots would scramble to take off. As they bumbled down the grass runway, engines open at full throttle, trying to take off on a short, bumpy track with a full load of fuel and ammunition, their heart would stop when the engine mis-fired. Was the fuel mix too rich, or too lean? They'd look at the control for the mixture and wonder which way to turn it. The right way would increase engine power and make lift-off straight-forward. The wrong way would lose power, and there was rarely enough time to fix the mistake. Read more: Software Checklist 2013/02/10 NASA Space CrewsI was watching some documentaries on the NASA space missions, and I started to realise that in the Apollo missions many of the crew were experienced, but some were not. This made sense, because you need to train new people and give them experience, but equally, it was important that some experienced members be on each mission. So I drew a diagram - see what patterns you see. Read more: NASA Space Crews ... 2012/11/06 The Birthday ParadoxIf there are just two people in a room, it's very unlikely that they will have the same birthday. On the other hand, if there are 1000 people in a room, it's absolutely certain that there will be shared birthdays, as there simply aren't enough days to go round without repeats. So as we add people to a room the chances of a shared birthday rise from 0 to 1, and at some point will pass through the halfway mark. When? And what does this have to do with cryptographic hash spaces? Read more: The Birthday Paradox ... 2012/04/17 The Trapezium ConundrumClear, precise, unambiguous and useful definitions are hard to come by in the real world. In maths we have the luxury of creating definitions that we want, and then chasing down the consequences. If the definition doesn't produce what we want, we can change it. But even things, things aren't always as easy as we might hope. Read more: The Trapezium Conundrum ... 2012/02/20 Revisiting The AntSo last time in The Ant And The Rubber Band we were talking about an infinitely patient ant walking on an infinitely stretchy rubber band. If you haven't already, you'll need to read that. So here's what's happening: Read more: Revisiting The Ant ... 2012/02/09 The Ant And The Rubber BandThere's a 1 metre long rubber band, and an ant, standing on it at one end. The ant starts walking along it at a speed of 1 cm/min. Every minute the rubber band is stretched (uniformly and instantaneously) to be one metre longer. The question is this: Will the ant ever get to the far end? Read more: The Ant And The Rubber Band ... 2011/12/20 Irrationals ExistFor this post I thought I'd have a quick diversion into talking about the so-called "Real Numbers." Upon reflection, however, I found that there was so much I wanted to say that there was no way to fit it sensibly into a single post. So instead I'll put some preliminary comments here, and then expand on them later. In particular, I'll give an explicit proof that for every interval you choose of non-zero length, there is an irrational in it. Read more: Irrationals Exist ... 2011/11/15 Multiple Choice Probability Puzzle
The immediate thought is - there are four options, so if I pick one at random then each has a one in four chance of being chosen. That means the answer is 1/4, or 25%. But that doesn't work ... Read more: Multiple Choice Probability Puzzle ... 2011/10/28 Random EratosthenesWhy do people think of the primes as somehow being "random"? What does that mean? How can we investigate? In this post I'll talk about a way of generating primes, and then see what happens when we toss in some randomness, just for fun. Read more: Random Eratosthenes ... 2011/09/13 Wrapping Up Square DissectionWe now have five valid dissections, and one "dissection" that might be regarded as invalid. So what do we mean by "a piece" and just how many dissections are there? Read more: Wrapping Up Square Dissection ... 2011/08/08 Dissecting A Square Part 2So we return to the square. It's simple enough to cut it up into identical pieces so that all the pieces touch the centre. But in how many ways? I rapidly got 5 (or 6, depending on a technicality), and I started to wonder about a proof that 5 (or 6) was all of them. I posted a badly worded question on an internet forum, and rightly got flamed for it, but in the answers was a shock. There was an infinite family of solutions. Read more: Dissecting A Square Part 2 ... 2011/07/26 Dissecting A CircleSo last time I talked about the three possibilities we have when we dissect a square:
What about the other possibilities? Read more: Dissecting A Circle ... 2011/06/01 Dissecting A Square (Part 1)Some time ago, mid-2009 I think, I was given a challenge that I found fascinating. You might choose to have a think about it, and here is the way I introduce it to people:
2011/05/24 An Oddity In Tennis(Part 3 of Decision Trees In Games) ... in which we discover that the techniques we've developed over the past two posts lead to an apparent anomaly in the behaviour of the scoring system, and ask "Why is it so?" Read more: An Oddity In Tennis (Part 3 of Decision Trees In Games) 2011/05/18 Decision Tree For Tennis(Part 2 of Decision Trees In Games) In the last post we analysed a simple "First to Two" (or "Best of Three") game of probability. More interesting, and more difficult, is something like tennis, which adds the complication of "Deuce." In tennis, the winner of a game is the person who not only has at least 4 points, but is also at least 2 ahead of their opponent. When you each have 3 points the next winner of a point doesn't win the game - they need to get two in front. Read more: Decision Tree For Tennis (Part 2 of Decision Trees In Games) 2011/05/15 - Decision Trees In Games (Part 1)A fairly standard exercise in probability is to ask who, under a given scoring system, will win a game given the probability of each move. For example, suppose we toss a coin, and I get a point for every head, and you get a point for every tail. Winner is first to 2. It's easy if the coin is fair, because the game is symmetrical. It's easy if it's a two headed coin, or a two tailed coin, because then the winner is certain. But if the coin shows head with probability p (and tail with probability q=1-p ) then it's harder. Read more: Decision Trees In Games (Part 1) 2011/05/09 - A Matter Of ConventionA friend of mine, James Grime, is becoming quite well known both for his mathematics presentations, as well as for his videos on YouTube. He's really quite good, but recently he complained that he was getting a lot of requests to settle a matter. He didn't really want to talk about it, but it's this: What is the value of 6/2(2+1) ?? Read more: A Matter Of Convention 2011/04/21 - Do You Nourish Or TarnishThere are people I know who are like the sunshine in the morning of a Spring day. They illuminate, warm, nourish, and make one's life better. There are others, though, who aren't like that. They see only what's theirs, ... Read more: Do You Nourish Or Tarnish 2011/04/18 - Binary Search Reconsidered"Binary Search" was made popular as an interesting test problem by Jon Bentley in his book Programming Pearls. There he says that it's an interesting problem, and baits the hook ... I was stupid - I claimed: "There is a simpler invariant and simpler code that together have a few advantages" ... Read more: Binary Search Reconsidered 2011/04/14 - Two Equals FourHere's a cool puzzle.
Consider the equation
Because the exponential tower is infinite, we can also write it as
But the part in brackets is the same as the whole, and hence is equal to 2. Thus we have 2=x2 Read more: Two Equals Four 2011/04/11 - The Lost Property OfficeLast week I gave a talk in Stroud. Well, three talks, actually. Two were my regular juggling talk, and one was a maths talk. They seemed to go well, with lots of nice comments from both the teachers and the students. It was a warm, sunny day, so as my host was going to be busy for an hour or so before taking me back to the station (an arrangement we had agreed in advance, and with which I was perfectly content) I decided to walk, ... Read more: The Lost Property Office 2011/04/05 - The Forgiving User Interface
Read more: The Forgiving User Interface 2011/04/03 - Setting Up RSSAfter saying that I would be Withdrawing From Hacker News I posted a note there saying so, and pointing people at my "blog" in case they wanted to read what I write in the future. Then someone asked if I could set up an RSS feed, so I've attempted to do so. Read More: Setting Up RSS 2011/04/03 - Withdrawing From Hacker News866 days ago I came across some essays by Paul Graham. I was interested in and impressed by some of the articles, but also realised that they were interconnected. To explore their interconnectedness I extracted all the links between them, graphed the connections, and computed a Google-like ranking. The results weren't actually that interesting because the essays don't cross-link much, but I sent them to Graham in case he thought they were interesting or useful. Maybe he would put more cross-links in, which might make the essays more of a resource than they already were. Slightly surprisingly, I got a reply, in which he suggested that I submit the link to Hacker News. I'd never heard of Hacker News, but had a look, thought it interesting, and submitted the link. Read more: Withdrawing From Hacker News
2011/04/02 - Colin's BlogI've been rethinking and reorganising my "blog". I've decided that each entry should be a separate page, and then the pages can chain forward, backward, and give a list of recent posts. We'll see how that goes. |



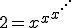 and suppose we want to solve it for x.
and suppose we want to solve it for x.
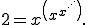

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email