
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
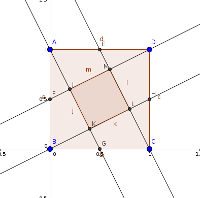
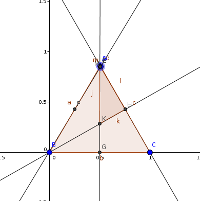
2016/09/18 - An Unexpected FractionOn 2016-09-09, @MEIMaths tweeted an image and said:
The way the question is phrased makes you feel two things. Firstly, you have to feel that the answer is likely to be surprising in some way, so that means it's likely to be a nice puzzle. But secondly, it seems clear from the phrasing that the answer must be the same regardless of the particular quadrilateral chosen. Well, I've seen this before in the context of a square, and the answer there is lovely - it's a fifth. The proof in the case of a square is fairly simple, and there are a number of ways of going about it. So there we are, it's sorted, the answer is a fifth. Nice one.
So what's going on? The short answer seems to be that @MEIMaths mis-spoke themselves, and despite the wording, they didn't actually mean any quadrilateral. But what might they have meant, and what answers might be possible? So here are some interesting questions:
ReferencesHere's the original tweet: Adam Atkinson has created a GeoGebra twitchet you can play with:
CommentsI've decided no longer to include comments directly via the Disqus (or any other) system. Instead, I'd be more than delighted to get emails from people who wish to make comments or engage in discussion. Comments will then be integrated into the page as and when they are appropriate. If the number of emails/comments gets too large to handle then I might return to a semi-automated system. That's looking increasingly unlikely.
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email