
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Wrapping Up Wrapping Up the EarthWe're coming to the end of this series. Our friend has purchased too much rope, too little rope, too much miraculous wrapping sheet, and now, finally, we come to the question of too little. But first, let's look at the different "rope" scenarios, and see what happens in each of the analogous "sheet" cases. The Rope Around the Earth problemWe have 6 metres too much rope, and having joined it in a circle we proceed to prop it up the same height everywhere. How high will that be? It turns out to be about a metre, regardless of the size of the Earth! That's a very surprising result for most people, but the sums are irrefutable. We also perform some "back of the envelope" calculations to refine the answer here: The analogous version for wrapping the Earth and discovering that you have a million square metres left over gives us a height of just 6.25mm, and that does depend on the size of the Earth. Sums: Wrapping The Earth The Other Rope Around the Earth problemNow instead of propping it up everywhere we prop it up in just one place with a tent pole. Turns out, that's quite a tall tent pole. The sums are here: That does depend on the size of the Earth, but perhaps the fun part about this is that we can again do this on the back of an envelope, once you approach it the right way. The analogous version with the wrapping is a bit more difficult, but it yields before too long, and gives a surprisingly elegant result that once again, just like the original Rope Around the Earth problem doesn't rely on the size of the Earth:
The $(Other)^2$ Rope Around the Earth problemOK, this one is silly, where the rope turns into a rigid ring that encircles the Earth, and we ask what happens. You can read about that here: The analogous "Wrapping" version has the Earth floating inside a rigid shell, and we ask what happens. That, however, is answered by The Shell Theorem, which we discuss in The Ring Of Steel, so we won't spend any more time on that. The $(Other)^3$ Rope Around the Earth problemThe rope is now too short, so we fuse the ends and throw the loop over the Earth like a lasso or quoit, and ask how close it gets to the equator. The actual calculations are here: We can ask for an equivalent with the wrapping problem, and the closest I can think of is to leave a gap around the equator and ask how wide it is. But that's genuinely trivial. We need an area of a million square metres, and the circumference is 40 million metres, so the answer is about an inch (in old money) or 25mm. That doesn't seem very interesting. We could instead leave a hole at the North Pole. Assuming the Earth is flat enough at that location, the hole would then be a circle of radius $R = \sqrt{10^6/\pi}$, which is interesting, as it is the height we computed for our Yurt in The Other Wrapping The Earth Problem, which seems a rather odd coincidence. Hmm. The $(Other)^4$ Rope Around the Earth problemBut now we come to the remaining case, where for the rope version a hole is drilled through the Earth as a short cut to save the 6 metres, and we ask how deep that will be. You can see that here: So what is the equivalent for the wrapping problem? Surely now we cut off a cap, perhaps at the North Pole, and ask how deep that will have to be. So let's do that.
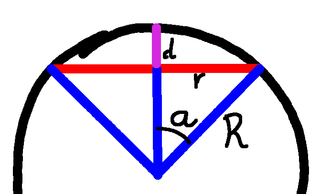
Cutting Off the CapWe are removing the cap, here shown at depth $d$ and radius $r$, and replacing it with the circle of radius $r$. So we need to know the area of the cap, the area of the circle, and the difference has to be our material deficit of a million square metres. But we know from the Archimedes Hat Box Theorem that the area of the cap will be $\pi(d^2+r^2)$, and the circle is just a circle, so its area is simply $\pi r^2$. So the difference is just $\pi d^2$. That seemed a bit easy.
Which I find oddly satisfying. There are still questions to answer here, such as why this result is identical to the previous, and whether we can get any sense of why this result is independent of the size of the Earth, but at this point I think it's probably time to change topic. Not sure what to ...
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email