Wrapping up Square Dissection - 2011/09/13
If you haven't already, you might want to read:
We're talking about dissections of squares and circles into
congruent pieces. That means the pieces are all the same
size and shape, although they may be mirror images of each
other.
Boundaries duplicated
Boundaries uncoved
Three piece "solution"
One piece of the 32 dissection
|
So last time I said that there are lots of ways of dissecting
a square into congruent pieces, all of which touch the centre.
One of the commentators - PMR - provided an image showing five
"classical" dissections (including one I didn't previously have!)
and one which could be regarded as potentially valid, but questionable.
So what is a valid dissection?
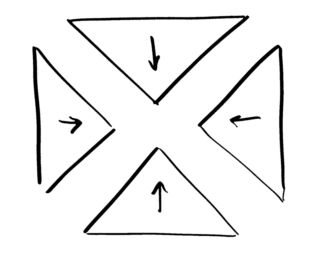
The obvious thing is to think of the shapes we get when we chop
up the square. At right is an example where we've cut it into
four triangles by cutting along the diagonals.
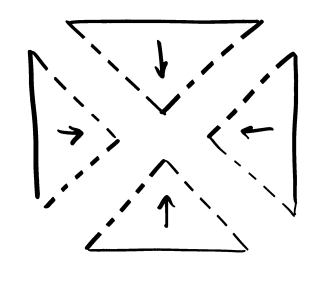
We can put these four pieces together to make the square, but
the boundaries get covered twice. We could try not including
the diagonal boundaries, but then they don't get covered at all.
And even if we include some and not others, there's always the
problem of the centre point.
So what do we do?
We could just say that the fiddly bits don't matter. More
technically, we could say that any set of measure zero
(effectively anything without area) can be covered twice, or
not at all, and we don't care.
Thus a dissection is a collection of sets
whose union is the entire square, and
whose intersection is a set of measure zero.
|
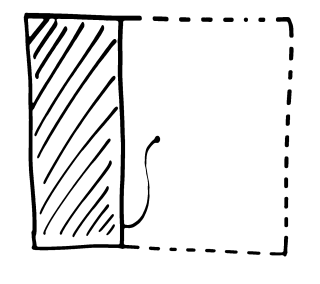
That seems OK at first glance, but a bit of creativity shows a
problem. We can end up with a three piece "valid" solution, as
shown at right. That doesn't capture our intuition at all.
In fact, here's another "dissection". For every point in the upper
left quadrant, consider it and its friends under rotation by 90 degrees.
Starting with any one of them, colour them clockwise red, green, blue and
yellow. In this way each "piece" can be dense in the entire square,
by which I mean that every circle drawn anywhere on the square will
contain some of each colour.
More particularly, the lower right corner can be "touched" by each
piece (by which we mean every circle around the lower right corner
contains at least one point from each piece). If we then think of
this as just the upper left quadrant of a square, and replicate it
four times using four new colours each time, suddenly we have a 16
piece solution! But again, it doesn't capture our intuition.
Somehow we want or need to exclude the "dust" types of pieces.
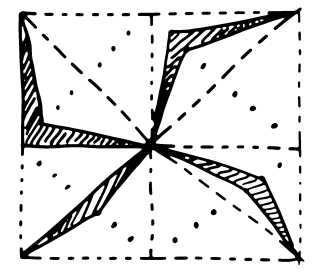
What if we consider a piece as being the closure of the interior.
That eliminates the "dust" type pieces, because they have no
interior, and it still allows pieces that have a "cut point". Now
we would permit the 32 piece solution, one piece of which is
"The Windmill" shown at right. Four "Windmills" in rotation cover
half of a square, reflect and we have another four. All eight
pieces touch the bottom right corner. Repeat four times around
that point and we have a 32 piece solution.
But should we allow pieces that have a cut point? Perhaps some
people might feel that they are "not true pieces" in some sense.
And that brings us to the classical definition, where a "piece"
is defined entirely by its interior, which must be connected.
(I believe that will also imply "pathwise connected", although
I'm not sure.)
| 




 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email