
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Minimal graphs with exactly C cycles ...Back in late August (the 26th to be precise) Chris Purcell (@ccppurcell@mathstodon.xyz) posted[0] the following:
The first few values are easy enough to compute by hand, but it gets quite tricky quite quickly. How can one construct a (simple undirected) graph with exactly 5 cycles?
Exploring the problemWe start by taking a few small graphs and counting the cycles. For a triangle we have exactly one cycle. For a square we also have exactly one cycle, but we have a smaller example for that, so we are not interested in the square. A square with one diagonal has two cycles of length three, and one cycle of length four, giving 3 cycles in total.
Constructing an exampleTo construct a graph with exactly $k$ cycles we can take $k$ triangles with a shared vertex. That gives the desired $k$ cycles with $2k+1$ vertices, but perhaps we can do better. To get 5 cycles, for example, we could start with a square with one diagonal, which has three cycles. Then we add two extra triangles, again sharing a vertex. That gives us the desired 5 cycles using only 8 vertices instead of 9. So we now know that $V(5) <= 8$. Can we do better? In fact, no, but proving so seems to be a trifle awkward. So we have a few questions:
But in general we can accomplish many cycles with many fewer vertices. User 0xDE (@11011110@mathstodon.xyz) made the following observation[1]:
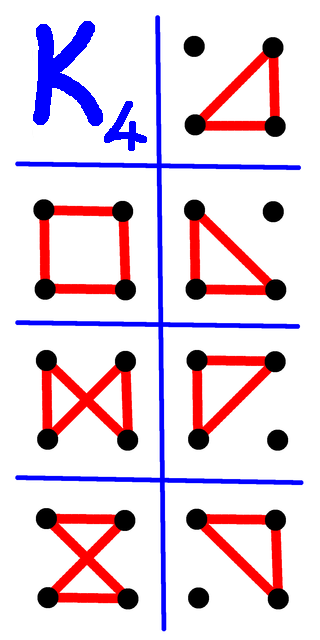
So we can get many, many cycles with not many vertices, but we won't necessarily get all possible number of cycles. With four vertices we can get 0, 1, 3, or 7 cycles, but not 2, 5, or 6. Even so, the required number of vertices certainly won't grow quickly. The complete graph on $k$ vertices has more than $(k-1)!$ cycles, and that's a lot.
What I did ...
The next step with my existing program would be to compute the number of cycles for all 1 billion connected non-isomorphic graphs on 11 vertices, but I estimate that would take around a week of runtime, so it's time to stop and wonder what the next interesting question might be. I'm happy to provide my code to anyone sufficiently interested, or to describe the process and algorithms in some detail in case people would like to implement them independently, but to be honest, they're none of interesting, clever, or innovative.
The OEIS ...The sequence is now in the OEIS: I have the first 18900 values in case anyone wants them.
AddendumI've had some feedback on this post, which has been absolutely brilliant, but I'm keen to get more. Did you find this easy to read? Was there something that confused you? Do you want to know more about some part of it? The comment box can be completely anonymous, or you can put your email in the appropriate place if you'd like a reply. Alternatively, ping me on Mathstodon or Twitter. I know I don't always hit the mark for level of detail, so please, do let me know.
Links
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email