
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Recursion ...It has been said that there are two hard problems in computing:
Variables
A variable has a name, and it holds a value. Some people seem never to actually get that idea, and mistakes they subsequently make can often be traced to a non-understanding of this. But most people seem to get the idea, either immediately, or after a small amount of practice. It has to be said, though, that in some modern languages the situation starts to get murkier. Sometimes a variable doesn't actually hold the value, it pretends to hold the value, and instead holds a pointer to the value, and the value itself is somewhere else. Then more than one variable can point to the same value. Some languages, Python for one, hide this implementation detail from you, so when you mutate the value via one variable and discover that the value "in" another variable has also changed, that can be a little surprising. And it gets even more complicated, but I'm not going to go there. The Function
Actually, sometimes you don't actually give it anything and it gives you back a value anyway, and sometimes it doesn't give you anything back! Yes, a "function" in computing can be a interesting beast, and is definitely different from a mathematical function. This can be even further complicated by the fact that sometimes you want your black box to have a memory, and in those cases even if you feed it the same thing multiple times you get different things given back to you. But in essence, in computing a "function" is a thing you refer to. You give it values (most of the time) and it does something, which might include giving you something back. Seems straight-forward, but for some people it just remains a complete and total mystery as to what's going on at all. Interestingly, I've found that some people have the same stumbling block in mathematics. They can "do sums" but the abstract concept of a "function" seems to defeat them. In some cases, for some people, it seems simply to be that they've never been exposed to functions in general and have always just dealt with formulas, but some people seem never really grasp the idea of a thing that takes things and gives you back things. Put like that it's perhaps not so difficult to see why they might have problems. Even so, for some people,"functions" are their Waterloo in the field of programming. RecursionNow we come to the third level of enlightenment: recursion. It seems to me, speculating idly and with no research to back me up, that recursion has similar conceptual challenges as Mathematical Induction and Proof By Contradiction. Perhaps the parallel with Mathematical Induction is fairly obvious, perhaps Proof by Contradiction less so, but stay with me for the moment. What is recursion?
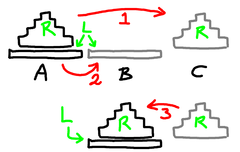
A similar problem arises with Mathematical Induction. Here we want to prove a proposition, but somehow we can magically use the truth of the proposition to prove the proposition. That seems to be obvious nonsense. How can we make sense of it? A specific example: The Towers of HanoiSo let's take a specific example, solving the Towers of Hanoi. We have three locations, A, B, and C, and a collection of disks of different sizes. Currently they are all stacked up in location A, and we want them instead to be in location B. But there are rules. Firstly, we can only move one disk at a time. And secondly, we may never put a larger disk on a smaller disk. Playing randomly with one of these for a bit shows that there is obviously some way of doing it, and some structure to the solution, but it would be nice to have a rigorous solution. And there is ... it goes like this. If there's only one disk then move it where you want it to go. Done.
So how does this work?The basic idea is this. Start by showing how to solve the simplest possible case. With this problem we've shown how to solve the problem when there is only one disk. Now consider any case, and assume (this is the bit some people find tricky) that we can solve all cases that are in some sense "simpler." If we can show how to break down the case we're trying to solve into a combination of simpler cases, then we're done. And that's what we've done above. We're confronted with N disks, and we assume that we can solve the Towers problem when there are fewer than N. We then observe that if we move N-1 disks out of the way (and we can, by assumption), move the last disk, then move the N-1 again (and again, we can), then we're done. So to make this work we need a few things:
Some more specific examples
So here we compute n! by saying that if n is zero then the answer is 1, otherwise we compute (n-1)! and multiply by n. In truth you would never compute factorial like this in real life, but it's a reasonable example of how the process works.
There are faster and practical ways, but this routine is here to demonstrate recursion. If you want to compute the Fibonacci numbers, don't do it like this. Really. Don't.
Imagine you have a bookshelf with books ordered by title, and you're looking for one in particular. You look in the middle and if what you're looking for is earlier than the book there, move left, otherwise more right. Here we have a list of objects, V, sorted from least to greatest, and we're looking for a specific item, K. The routine takes the key, the list, and a range [L,U) in which the item occurs, if it's there at all. The "lower" bound is inclusive, the "upper" bound is exclusive. Let's see how the code is structured. If the array is empty then the item isn't found, obviously. If there is only one item in the list then either our key is there or it isn't, and we return the appropriate result.
Returning to mathematicsThe connection between recursion (in programming) and mathematical induction is reasonably straight-forward. In each case we deal with the instance in front of us by assuming we can do simpler instances, and then using them to solve the one we have. What is the connection with Proof by Contradiction?
Our first failure can't be at n=1 because as part of a proof by induction we have proven our proposition is true in that case, so that means n>1. Now consider n-1. Since n is the first failure, the proposition is true for n-1. Because we have a proof by induction, we have a proof that if it's true for n-1 then it's true for n. So it's true for n. So assuming it fails somewhere leads to a contradiction. Thus we have used Proof by Contradiction to show that the steps of Proof by Induction suffice to show that something is true. Well, not quite. We've also used that there's a smallest case for failure, so that uses the Well Ordering principle, and so it goes on. Suffice it to say that these things are all connected, and some things are more obvious to some people, while other things are more obvious to other people. In short, it can be complicated, and when you first meet the ideas they can be a little daunting, and not at all obvious. For some people (perhaps nearly all of us!) it's only with time that they become easy and "obvious." ParallelismAnd so we have the fourth level of programming is the true understanding of parallel programming. We'll leave that for another time.
Send us a comment ...
|
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email