
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
The Other "Wrapping the Earth" ProblemIf you've been reading the previous posts you'll know the drill. This is a brief recap ... Our friend once again has too much to drink, and once again indulges in a little late night internet shopping. This time, however, it's fuelled by curiosity, having discovered that there's a material that is infinitely stretchy, but which always retains its area. So while you can stretch it one direction, it will shrink in another. We know the Earth's circumference is 40 million metres, so our friend purchases some 510 million million square metres of this wonderful material, expecting that it will be about the right amount to wrap up the Earth, and goes off to bed. It takes some time for the order to arrive - next day delivery wasn't available from this vendor - but when it does arrive our friend goes to it and heroically wraps the entire Earth, only to discover that there is slightly too much material. Just one square kilometre. One million square metres. Last time we looked at solving the problem by propping it up the same height everywhere, but that really is a lot of work. Much easier just to get a tent-pole and prop it up in just in one place. How high will that have to be? The sums ...
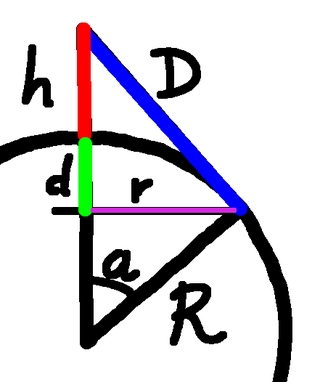
As always, the radius of the Earth is $R$. The area of the spherical cap that the fabric has been lifted from is $\pi(r^2+d^2),$ and the area of the "Yurt" is $\pi rD$. The first is from Archimedes Hat Box Theorem, and the second requires a little work, but is the formula for the area of the curved surface of a cone. So where do we begin? There are lots and lots of right-angled triangles in this diagram, so we could start by writing them down:
Now we return to $h=R\left(\frac{1}{c}-1\right)$, substitute $c\approx 1-a^2/2$ and simplify, and we end up with:
Using the resultFirstly, it amazed me somewhat that the result doesn't rely on the size of the Earth. In fact it does, but that's hidden in the small angle approximation, so we do need the Earth to be big enough. But even so, the result doesn't rely on the size of the Earth, so we can simply do the sums to find the height:
Can we avoid the calculator?It depends on what you know. I remember that $\sqrt{1/3}\approx 0.577$, so that's close to $\sqrt{1/\pi}$. We can get closer by remembering that $\pi$ is about 5% bigger than 3. We're taking a square root and dividing, so our answer should be about 2.5% smaller than 577. Taking 2.5% is dividing by 10, then by 4, so that's 14.4 (ish) and we subtract that from 577 giving a rough, back-of-the-envelope calculation of about 562 or 563. That's pretty close. AcknowledgementsMy thanks to Neil Walker and Colin Beveridge (Web site) for useful feedback and suggestions.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email