
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
2019/01/15 - The Other Rope Around the Earth ...The well-known "Rope Around the Earth" problem is lovely, and, as I say, well known. But some time ago David Bedford mentioned another rope around the Earth problem. A different rope around the Earth problem. And it goes like this. Our protagonist has gone onto the internet and purchased 40 million metres of rope, as you do, and then wandered around the Earth, stretching it out behind. As you do. The expectation was that it would exactly encircle the Earth, since the original definition of the metre was that the distance from the North Pole to the Equator, through Paris, should be 10 million metres. Alas, things didn't quite work out, and there was a six metre excess. Well, our protagonist didn't want to cut it, because it was expensive, and didn't want to tie a knot, because that would be ugly. So they fused the ends together, and wondered what to do with the slack. In the original problem it was distributed evenly around the Earth by propping it up a fixed distance everywhere, and the question is: How high will that be? But that's silly. Having gone all the way around the Earth once to put the rope there in the first place, who would go around a second time to prop it up?!? No, let's just get a tall tent-pole and prop it up here. Now a three metre tent-pole won't do the trick, because the rope will run up to it on one side, go up, come down, and go on its way, the 6 metres of slack being used. So the pole has to be taller than 3 metres. But how much taller?
So there is the question.
But the meta-question is this: Can you make the calculations simple enough to do in your head (or on a sheet of paper). No calculators. How close can you get? The answer continues here, but I strongly urge you to have a play with it first. For one thing, you might get a better answer! For another, if you've played with it for a bit you can follow along more easily. However, here we go ... The calculation
That means that the tangent on each side must be 3 metres longer than the arc length, so we have this equation:
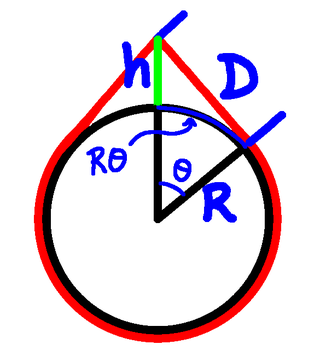
We start with the equation we had from the "Distance to the Moon" calculation, that provided $h$ is not too large (whatever that means), $D^2\approx 2hR$, where $D$ is the distance to the horizon, $R$ is the radius of the Earth, and $h$ is the height from which we are making the observation. We rearrange that to make $h$ the subject:
Substituting that into our equation about the length of the rope:
So multiply both sides by $R^3$ and we get:
Which is nice. Refining the numbersWe've made approximations all over the place, but most have been the small angle approximations, and they're pretty good - we'll see what $\theta$ is in a moment. The main approximation was to replace $\frac{81}{8}$ with $10$, an error of 1.25%. When we take the cube root, the error due to substitution is then about 0.41%, so our answer should be 0.41% bigger. That makes it $h\approx 401.64$, although certainly some of the decimal places are not justified. So our final answer is $401.64$ metres. So what are the actual numbers?Solving numerically we get $\theta\approx 0.01120332437$, and so $D=R\tan(\theta)$ is about $71704.276$. Now we compute $h$:
That'll do. How good are the approximations?So just how good are the approximations? We can have a look at the value of $\theta$. Our numerically derived value is $0.01120332437$, but the approximation is $\left(9/R\right)^{1/3}=0.01120351...$, so they agree to 6 decimal places, or 5 significant figures. That's pretty good. Then at that value of $\theta$ we can also compare $\tan(\theta)=0.0112037931200...$ with $\theta+\theta^3/3=0.011203793096...$, agreement to nine decimal places, or, as Rob Low says:
And finally ...Rob also suggested a slightly differ route to the answer. My calculation was done in my head, and I was able to use the formula for the distance to the horizon, because that was something I'd done earlier. And just as in the case of the Radius Of The Earth Part Two, that biased me to a particular way of working.
From the diagram:
Nice.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email