
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
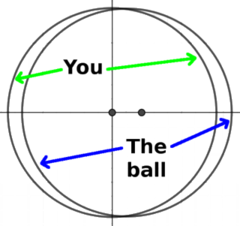
The "Fore-Aft" TideIn our last post we saw that when we're in orbit, if we throw a ball very gently in exactly the right direction, somehow it bounces back and forth through our position. We experience a fictitious force, pulling the ball back to a resting position, so it moves in Simple Harmonic Motion. So remember the setup. You're in orbit around the Earth with the International Space Station, and you have a juggling ball. (Don't ask). You hold it next to your helmet and release it, and it just stays there, apparently floating. Now gently push the ball ahead of you in orbit. In effect you are throwing the ball away from you, and once again, the expectation is that it will drift away from you in a straight line at a constant speed. And once again, it doesn't. So what happens this time?Well, it depends.
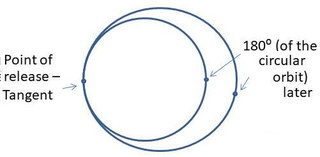
So if we throw the ball exactly tangentially, that's what happens. The ball ends up in an elliptical orbit, but it's a slightly slower orbit. So let's tweak our direction slightly, let's add a tiny "upwards" component. The throw of the ball is not exactly tangential, but it does end up in an elliptical orbit. More, we can arrange this angle so that the period of that orbit is identical to ours. If the throw is gentle enough the angle to our path is tiny. What happens then? Remember, we're assuming that we've injected it into an orbit that has the same period as ours, 92 minutes. This time the ball starts off travelling away from you, but again, it apparently slows down, and again, it comes to a complete halt in 23 (or so) minutes. Then it starts to come back. It passes you (or you overtake it) and it starts to fall behind. As last time it again slows down, comes to a complete stop, and returns. Because the orbital periods match, a complete cycle takes about 92 minutes, and if you have indeed got the direction exactly right (and that's inhumanly accurate, I admin) the ball will gently oscillate through your position, completing a cycle every 92 (or so) minutes. Again, Simple Harmonic Motion. But what's happening this time?
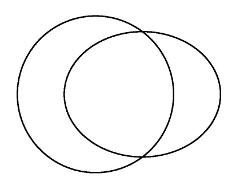
Now we use the fact that the orbital period is determined only by the length of the semi-major-axis, so provided the ellipse is as wide as the circle, the orbital period will be identical. Remember, we're assuming that our gentle "push" of the juggling ball hasn't altered its orbital period, so that means the "width" of the ellipse that it now has as its orbit must be same as that of the circular orbit. That, in turn, means that some of the ellipse will be outside the circle, and some inside. The result is that the paths will cross twice. In one case the ball will depart forwards, and in the other we will overtake the ball. Another way to understand itCan we understand this in simple, local dynamics? Yes. By pushing the ball ahead of us we are giving it a little more speed, so it will rise into a slightly higher orbit. But now it doesn't have enough speed to stay at that greater altitude, and while it initially gets away, the higher orbit is a slower orbit, so we catch up. Then it falls to a lower, slightly faster orbit, catches up with us, and so the cycle repeats. This also requires that our "push" is not exactly tangential, otherwise we get the Hohmann Transfer Orbit as mentioned above. Tricky this, isn't it! From the outside looking in it's a simple case of slightly different, overlapping orbits with the same orbital period. But from our point of view it's as if there is a mysterious force pulling the ball back to us, and it bounces back-n-forth in Simple Harmonic Motion. Quantifying the forceSo how big is this mysterious force? Since the period of bounce is the same as the orbital period, exactly the same calculation works as last time, and we get exactly the same equation for the force. So in each direction, sideways and fore-aft, we have an inwards acceleration of about $1.3x10^{-6} ms^{-2}$ for every metre of displacement. Again, not a lot, but enough to have to know about in some cases. Comparing with gravitySome people wonder if the Simple Harmonic Motion is caused by the gravitational attraction of you, or of the Space Station. We can calculate what mass is needed to have the same attractive force at one metre. The formula is Newton's universal law of gravitation:
So no, the gravitational attraction of the ISS isn't really relevant. Whew! And next?In our next post we'll look at the remaining direction - "up" and "down". AcknowledgementsMy thanks to Neil Walker for doing the initial calculations of gravitational attraction, Ben Ashforth (Twitter) for a correction about the orbital period, and the "exaggerated" diagram, and Bill Mullins (Twitter) for conversations about transfer orbits, etc. Their contributions made this post much better than it might have been.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email