 Subscribe! Subscribe!

My latest posts can be
found here:
Previous blog posts:
Additionally, some earlier writings:
|
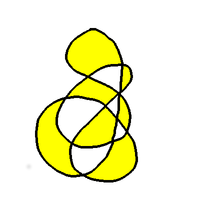
The Doodle Theorem
The Doodle Theorem says:
|
|
|
Any map drawn with a single pen stroke
that returns to its starting point can be
two-coloured. |
|
|
Here's one proof.
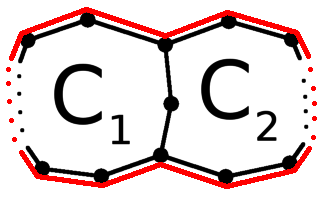
Take a planar graph that's been drawn with a single pen stroke
that returns to its starting point.
- As we draw the graph, for every vertex we must arrive, then
depart.
- Except for the vertex where we start and end, but we can
think of the final arrival as matched with the initial
departure.
- As a result, every vertex must have an even number
of edges.
- In the dual, a circuit around a vertex of the original will
have an even number of edges,
- ... because edges in the dual cross edges in the original.
- Consider two circuits that share edges but do not cross. When
combined into a single cycle, the length of the resulting
cycle is the sum of the two lengths, minus twice the number
of edges in the shared section.
- By combining the individual cycles in the dual around vertices
of the original map, we can now see that every cycle in the
dual is of even length.
Now we use the theorem that says:
- A graph is bipartite if and only if every circuit is even.
We'll come back to that in a minute.
|
An Euler Cycle is a tour of all the edges of a graph,
visiting vertices as often as necessary, but traversing every
edge exactly once, and returning to our starting position. |
So given all that, we now have that the dual is bipartite, and that
means both it and the original map can be bi-coloured!
So we're done - a planar graph with an Euler Cycle (see side box)
can be bi-coloured.
Well, nearly done. We still have to show that last step.
|
Theorem:
- A graph is bipartite
- Every circuit is even.
|
Proof:
It's enough to prove this for each component, so we may assume that
the graph is connected.
Pick any vertex $a$ and put it in $A.$ Repeatedly pick a vertex $v$
in $A$ and put its neighbours in $B,$ or pick a vertex in $B$ and put
its neighbours in $A.$
If a vertex is put both in $A$ and in $B$ (for the first time), that
gives us an odd cycle. If this never happens, then the sets $A$ and
$B$ form a partition of the vertices of the graph into two independent
sets; in other words, it is a bipartite graph.
And we really are done.
|
Comments
I've decided no longer to include comments directly via the Disqus
(or any other) system. Instead, I'd be more than delighted to get
emails from people who wish to make comments or engage in discussion.
Comments will then be integrated into the page as and when they are
appropriate.
If the number of emails/comments gets too large to handle then I
might return to a semi-automated system. That's looking increasingly
unlikely.
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email