
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Rounding up the ropes, and more ...We've seen the $(Other)^k$ rope around the Earth for $k=0, 1, 2,$ and $3$. In this post we'll look at $k=4$, but we'll start with a "heads up" for where we'll go next. We haven't yet done the analysis for $k=2$, i.e. The Other Other Rope Around The Earth problem, so we'll do that next. In the meantime, you might want to ponder this one ... The Sheet Around The EarthOur friend once again has too much to drink, and once again indulges in a little late night internet shopping. This time, however, it's fueled by curiousity, having discovered that there is a material that is infinitely stretchy, but which always retains its area. So while you can stretch it one direction, it will shrink in another direction. A quick calculation shows that if $A$ is the surface area of a sphere, and $C$ is its circumference, then $\pi A=C^2$, which is interesting. The Earth's circumference is 40 million metres, so our friend purchases 500 million million square metres of this wonderful material, expecting that it will be about the right amount to wrap up the Earth. It takes some time to arrive - next day delivery wasn't available - but when it does our friend heroically wraps the entire Earth, only to discover that there is slightly too much material. About one square kilometre, one million square metres. But that's OK - our friend decides to prop up the covering everywhere. How high will that be? We'll do that one soon. In the meantime ... The rope that was too short ...Alun Jones, not content to provide the $(Other)^3$ rope around the Earth problem, has also proposed a $(Other)^4$ version. In this version, having discovered that the rope is too short by 6 metres, our friend drills a straight hole through the Earth to create a short cut. At its deepest point, how deep is it? You may choose to ponder that. My initial reaction was that this is pretty much exactly the same as The Other Rope Around The Earth, because the triangles can be moved about, and the distances remain roughly the same. I was wrong, and you might choose to do the sums before reading on.
(scroll ...)
(scroll ...)
(scroll ...)
(scroll ...)
(scroll ...)
(scroll ...)
(scroll ...)
(scroll ...)
(scroll ...) Drilling the hole ...
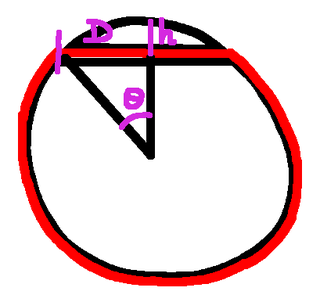
We need to shorten our total length by 6 metres, which means the arc length $R\theta$ has to be 3 metres longer than the direct distance to the halfway mark. Thus $R\theta=D+3$. We have a right-angled triangle, so $D=R\sin(\theta)$. Now we again use the approximation of $\sin(\theta)\approx\theta-\theta^3/6$, and we can expand, rearrange, and simplify to get $\theta^3\approx 18/R$. Square that and we have $\theta^6\approx 324/(R^2)$. Then we have $h+R\cos(\theta)=R$, and using $\cos(\theta)\approx 1-\theta^2/2$ we can simplify to get $h\approx R\theta^2/2$. Cube that and we have $h^3\approx R^3\theta^6/8$, into which we can substitute in our expression for $\theta^6$ above. When the dust settles we have: $h^3\approx 40.5 R$ Well, $10R$ is 64 million, and the cube root of that is 400, which is the answer we got for The Other Rope Around The Earth problem. But now we have an extra factor of about $(4.05)^\frac{1}{3}$.
And we're done - the answer is about 640 metres. You may choose to substitute that into the original equations to see how close we are. AnalysisSo why is this answer 1.6 times the answer for The Other Rope Around The Earth problem? I'll leave that to the (mythical) interested reader - let me know in the comment box. Next time, wrapping up The Other Other Rope Around The Earth problem, then after that, wrapping up the Earth. Sort of.
AcknowledgementsMy thanks (for some definition of the term) to Alun Jones (Twitter, Web site) for suggesting the problem.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email