
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Recursion revisited ... a specific exampleSome time ago I wrote a post on Thinking About Recursion, and more recently I wrote about a problem concerning the problem of the number of Vertices Required For Cycles. As it happens, the code for that problem is heavily recursive, and provides a great example of using recursion to solve a real problem. So I thought I'd show you.
The cycle problemThe problem in question is this:
The function $C{\rightarrow}N$ is now in the OEIS: But how are values computed?
Counting cyclesThe overall strategy is to look at all graphs on $N$ vertices and for each one, count how many cycles there are. Since we will be looking for the minimum number of vertices for a given number of cycles we can ignore graphs that are not connected, and we can ignore graphs that have a vertex of degree 1. So we look at all the non-isomorphic connected graphs of minimum degree 2. But at its heart, for a given graph we need to count how many cycles it has. Here is the algorithm. We define routine "count_cycles" which takes a graph in the form of a list of edges. There are more efficient data structures for this algorithm, but for the purposes of describing it we'll stick with this one. Routine "count_cycles" is a recursive routine. If there are no edges then the answer is 0 ... there are no cycles.
Otherwise we can select an edge. In principle we could find some clever heuristic for choosing the edge, but in practice we simply choose the first edge from the list. Even so, we call out to a routine to make the choice:
Every cycle either does include this edge, or does not include this edge. So we remove it from the graph:
Then count the cycles in the graph without that edge. To do that we simply call this routine - this is the first instance of recursion.
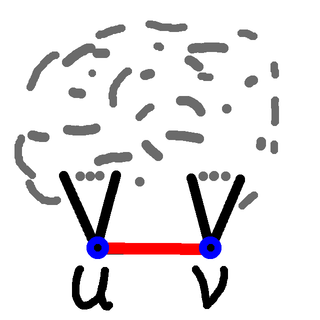
Any cycle that contains this edge $(u,v)$ will then consist of the edge, and a path from $u$ to $v$. So having earlier removed the edge $(u,v)$ we can now count the number of cycles by counting the paths from $u$ to $v$ in this reduced graph.
We then put the edge back, and return the total:
That's how we count the cycles, and all that's left is how to count the paths from $u$ to $v$.
Counting pathsSo now we have to write the code to count the paths from $u$ to $v$:
If $u$ and $v$ are the same vertex then we have one (degenerate) path:
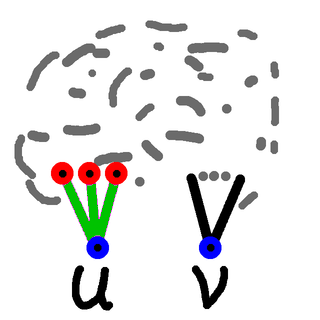
So we can remove the green edges, and for each of the red vertices we then count the number of paths from that to $v$. So let's get our list of green edges, and remove them:
Then we get our list of red vertices.
The total number of paths from $u$ to $v$ is the total number of paths from the red vertices to $v$. So we take that total by a recursive call to this same routine:
Finally, we put all those edges back, and return our result:
SummarySo here is the code complete. The routine "count_cycles" calls itself recursively, and also calls "count_paths". In its turn the routine "count_paths" calls itself recursively, and we're done. With any recursive routine we should always ask: How do we know the recursion bottoms out? The answer in this case is that in every call the number of edges decreases, is a whole number, and cannot go below zero. Because of that, in each case the call tree has to terminate. And the code isn't that big, nor that complicated. This is the power of recursion when appropriately applied.
End NotesThis is not intended to be especially efficient code, nor is it particularly good Python code. That's not the purpose (in this case). The final version was more efficient, but less clear due to the modifications made for that efficiency. Even so, I hope the algorithm, and how the recursion works, is clear.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email