
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
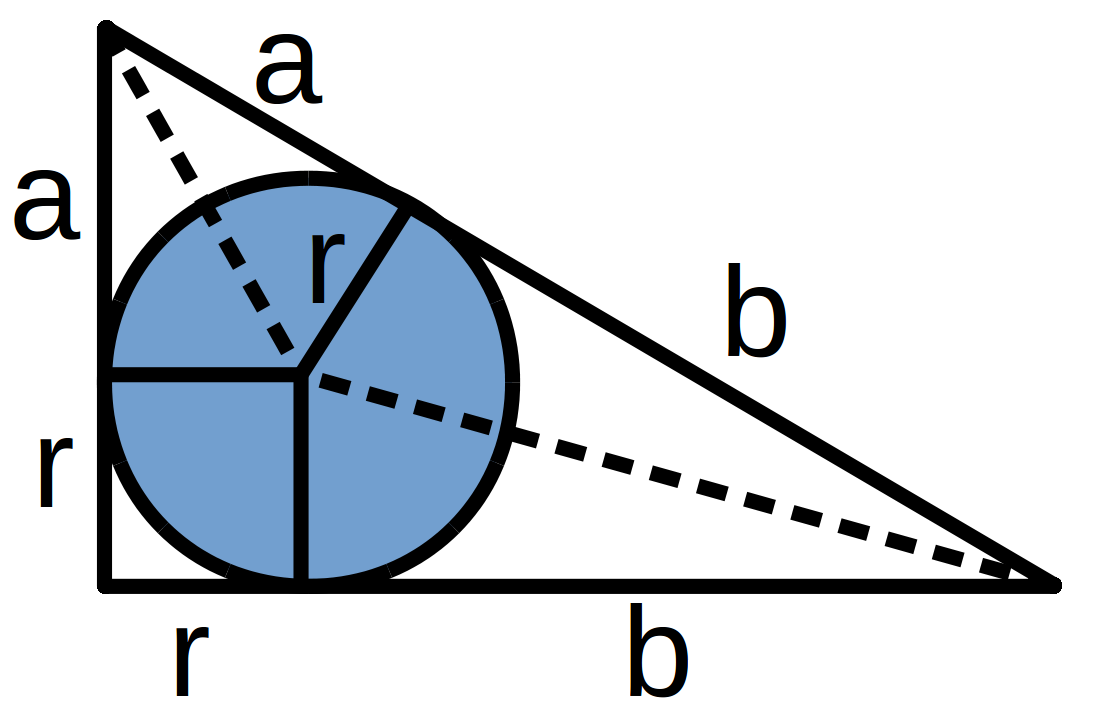
An old proof, rediscoveredSome time ago I was working on a puzzle about incircles, and unexpectedly a proof of Pythagoras' Theorem dropped out! I'm sure it's well known to people who know lots about Pythagoras' Theorem, but I thought I'd share it.
Let's think about the area of the triangle. On the one hand it's $\frac{1}{2}(a+r)(b+r),$ but on the other hand it's the square plus each kite, which is $r^2+ar+br.$ That is not instantly obvious, but is left as an exercise for the interested reader. It might help to remember that the centre of the incircle lies on the angle bisectors. Equating these two expressions for the area we get
Multiply through by 2, expand and simplify:
So now let's ask about the square on the hypotenuse.
Substituting in the value for $ab$ we get:
Rearrange:
So:
And we're done.
CommentsI've decided no longer to include comments directly via the Disqus (or any other) system. Instead, I'd be more than delighted to get emails from people who wish to make comments or engage in discussion. Comments will then be integrated into the page as and when they are appropriate. If the number of emails/comments gets too large to handle then I might return to a semi-automated system. That's looking increasingly unlikely.
|
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email