
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Poking The Dusty Corners - 2015/04/14In chatting with people about what a maths degree is, and what it does for you, I've often been intrigued by a particular response. I've shown them something that they expect to be true (or false) and then shown that their expectations can be confounded. When I do that, a common response is "Well, you're just being stupid." This is common enough that I thought I'd write a little bit about it. See, in this case what they're calling "stupid" is something that I call "intriguing". What they're discovering is that so far they've only met "nice" and "normal" things, and that there are things out there that are not "nice," not "normal," and which do not behave in the way they expect. So let me give you a simple example.
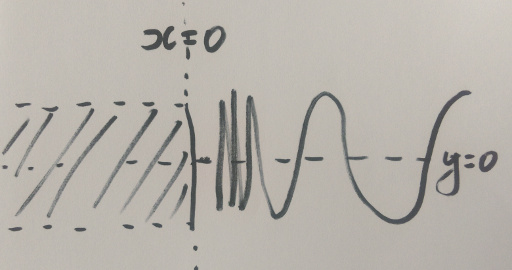
So far so good. So if we have a set of points and there is no way we can draw a disconnection, no way that we can draw a line separating the points into two (or more) regions, then the set of points must obviously be connected. So let's take a specific example. Let's take all the points (x,y) that satisfy the equation:
and let's additionally take all the points (x,y) where x<=0 and -1<y<1. What does that look like? Well, something like this:
So there's no disconnection, but it's not "connected" in the usual sense of the term, because we can't walk from anywhere to anywhere. It's at this point I usually get the response:
And this is what a maths degree is actually about. It's about being able to be precise, and to be sceptical about things that look reasonable, but which don't have a proof. It's about being able to follow a long chain of reasoning, and to know whether or not the argument is sound. Usually the things being reasoned about are abstract, and then the techniques have a value of their own in possibly unexpected ways, but it's really the reasoning itself that is the real prize. So when something comes up that you don't expect the best response is not "Well, now you're just being stupid." but instead is:
It's hard to get this right, and it's hard to develop these skills, but nothing worth having comes for free, and it's those abilities that make the maths degree of value no matter where you end up in your life and career.
CommentsI've decided no longer to include comments directly via the Disqus (or any other) system. Instead, I'd be more than delighted to get emails from people who wish to make comments or engage in discussion. Comments will then be integrated into the page as and when they are appropriate. If the number of emails/comments gets too large to handle then I might return to a semi-automated system. That's looking increasingly unlikely.
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email