
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
2019/01/29 - The $(Other)^3$ Rope Around the EarthSo we have:
(I can hear some of you groaning from here)
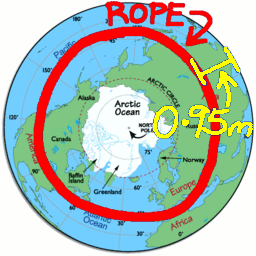
Our protagonist again has too much to drink and again gets involved with internet shopping, and again orders 40 million metres of rope to girdle the Earth. But this time, upon travelling all the way around the Earth, trailing the rope behind, it's six metres too short! Argh! OK. It won't stretch, we could cut six metres off the other rope, but that's now a tourist attraction, so we need a different solution. Aha! Let's move it slightly to the North, to a slightly higher latitude, and run it around one of the parallels of latitude. It will still be a circle, but it won't be a Great Circle. We can picture this as joining the ends of the rope to make a loop, and then throwing it over the Earth. It's too small to fall off, so it gets stuck part way down.
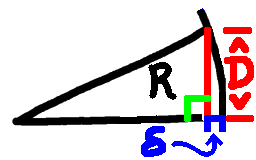
We can go about this in the obvious way, writing down the formula and using algebra to solve it. It's powerful, and we can solve most things like that. But there is no insight, no connection to other problems. The straight-forward algebra versionSo we need to know the circumference at a given latitude. That's not hard. At latitude $\theta$ we can picture the circle, and it has a radius of $\cos(\theta)$. So we want $C\cos(\theta)+6=C$, where $C$ is the Earth's circumference. Rearrange and we have:
Based on that, our actual distance north of the Equator is given by $R\sqrt{12/C}$. But $C=2\pi R$, so simplifying a little that can be re-written as:
But wait - there's more!In truth, we can do this in a completely straight-forward manner, and it's really not that hard.
But what's the answer?Approximating $6/\pi$ by 2, and ignoring the "million", we want the square root of 12.8. But $(3.5)^2$ is 12.25, so the answer is about 3.5. But wait! 12.8 is about 5% bigger than 12.25, and $\pi$ is about 5% bigger than 3, we're multiplying by one, dividing by the other, so these two errors compensate. The answer really is about 3500 metres. More elegantly ...So is there a more elegant way to do this? (Of course there is, otherwise I wouldn't've asked ...) I was struggling with this, then over lunch Rogerio Martins made a comment that provided the necessary insight to be able to solve this neatly, cleanly, and without long, complex calculations. So how does that work?
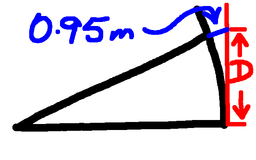
Keeping that in mind, we switch to a side view. Now we see the rope some distance above the equator, and ask what that distance is.
But we have enough information to do that! (Well, I have - and so will you if you've been following along in this series.) When we are 5 metres up, the distance to the horizon is 8000 metres. It goes as a square root, so we halve the distance by being only a quarter as high, so from 1.25 metres we can see 4000 metres. Not quite what we want, so do it again ... from 0.31 metres (roughly) we can see 2000 metres (roughly). Now we cheat a little and say that 0.31 is about 1/3 of 0.95, so we are increasing our height by a factor of three, and that increases our distance by a factor of $\sqrt{3}$. That's about 1.732...
And again, we've done that without calculators, tables, computers, or any aids. That gives me more pleasure than perhaps it should. You might like to do the sums on a calculator and see how close these results are, and where the errors are worst. Can you do better? Let me know ...
AcknowledgementsMy thanks to Alun Jones (Twitter, Web site) for suggesting the problem, Rogerio Martins (Web site) for his insight that led to the solution, and Adam Atkinson and Pedro Freitas for feedback, comments, and corrections.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email