
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
(One of) My Favourite Puzzle(s)It is impossible to choose a single problem as my favourite. There are so many, each with their own attractions, each with their own charms. But there is one that I solved quickly, and then found that I had only just started to scratch the surface.
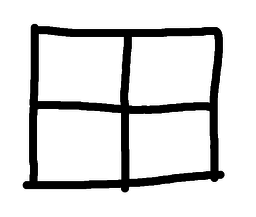
As you probably realise, this isn't hard. The solution shown here is the usual first guess, but there are others. I've shown some here below.
Are there any more? Well, as it happens, yes, there are. Here are some more:
So the solutions with 2 pieces and the solutions with four pieces have versions where the cuts are curved. In a sense, all the solutions with two pieces are essentially of the same form: one cut goes out from the centre to the edge, and then that cut is rotated by a half turn. If the result doesn't self-intersect, it's a solution. Similarly, all the solutions with four pieces are of a similar form, but with quarter rotations. So we appear to have characterised all these solutions with two or four pieces. Now we have two questions:
Warm-up, stage two ...
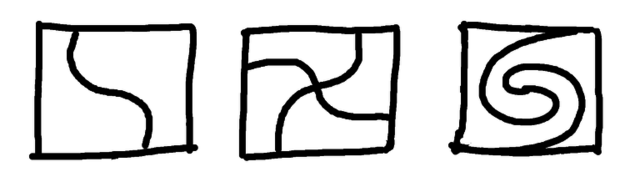
And all these solutions have straight lines. Are there any solutions with curved cuts? So:
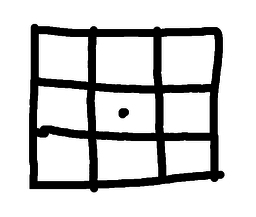
Warm-up, stage three ...So we have seen solutions where all of the pieces touch the centre point, and we have seen solutions where one of the pieces touches the centre point (and hence must contain the centre point), so we wonder if there are any solutions where some pieces touch, and some pieces don't. Specifically, are there any solutions where two or more pieces have the centre point on their boundary, but one or more pieces are not in contact with it? This is not difficult - but remember that the pieces must all be the same size and shape. They must be congruent. Then having found a solution, and then perhaps finding several solutions, can you find solutions with curved cuts? So:
Warm-up, stage four ...So for the square we have looked at dissections with:
What about:
Are you sure? Finally, the puzzle ...Consider the circle. We can get a dissection of the circle into identical pieces that all touch the centre. Simply slice it like a pizza, and then perhaps add a little flair to use (identical) curved lines rather than the simple straight lines. Is there is a dissection of the circle into identical pieces where the centre point is in the interior of a piece? I can tell you for free that this is an open problem - no one knows the answer for sure. But here's the puzzle:
But there's more ...When I was first presented with this problem (and without the warm-up) I quickly sketched a solution and handed it over. My companion was disappointed that I had solved it so quickly, but we moved on. Later I received an email saying that another group had a different solution. I was sceptical, but it turned out yes, there was another solution. Mortified that I had given up so quickly I worked hard and produced an infinite family of solutions. More, for each "level" of that infinite family I had multiple solutions, starting with a few but increasing rapidly. I had found an exploding infinite collection of solutions! And then there was my original. Then Joel Haddley found another solution. Working together we then generalised that into an infinite family. This was a "linear" family, but even so, an infinite one. And then there was my original. Sadly, we have now realised that my original solution (which in some circles (excuse the pun) is actually well known) is in fact the base case for this second infinite family. But we thought we had completed the problem. But no. A colleague of Joel's, Stephen Worsley, has now converted each of the solutions in this second family into a continuous family. In effect, for each solution in this second family there is a dial you can turn to create an infinite collection. So now we have an exploding countably infinite family, and a linear countably infinite family of uncountably many solutions, and we still don't know if there is a solution where the centre is in the interior. But even if all that meant nothing, here is a final puzzle. Can you find solutions where:
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email