Latitude Correction

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

2019/01/01 - The size of the Earth, a correction.

Recently I've been discussing the details of measuring the size of the Earth by watching a shadow descending a wall at sunrise, or ascending at sunset. The sums are easy enough if you do it at either Equinox, and at the Equator, and you can read about it here:

https://www.solipsys.co.uk/images/EquatorAndLatitude.png

Equator in blue,
our latitude in red

The challenge then is to do it somewhere other than at the Equator. After all, you can choose your time of year, so you can choose to do it at Equinox, but you can't necessarily travel to the Equator. So how can we do it at a non-Equator location, a non-zero latitude?

Definition of Latitude
The observation that unlocks the calculation is that when we perform the procedure at some latitude, the answer we get is the size of the Earth at that latitude. So the number we get is the circumference of the circle that is the parallel of latitude. So to get the true size of the Earth we need to make a correction. But by how much?

Some work will show that the correction is to divide by the cosine of the latitude, so that's not too hard. But we do (obviously) need to know our latitude.

The setting Sun
Hmm. How can we do that? How can we find out our latitude?

Well, we're doing all this at Equinox, and at Equinox the angle from the vertical of the Sun's descent or ascent is your latitude. So we can set up a pinhole to cast an image of the Sun on our convenient wall, and measure the angle of its path from the vertical, and there is our latitude.

Finding our latitude
Well, that's all well and good, but, as my correspondent then remarked, I've now quietly slipped in the requirement for a protractor.

Hmm.

Ah, no, I don't need a protractor.

Computing the Cosine
Mark the path of the Sun's descent. Choose a point near the end, and from it draw a vertical using the pendulum as a plumb bob. From some point earlier in the Sun's path draw a horizontal, and now we have a right-angled triangle. On that we can measure the lengths of the adjacent and hypotenuse, divide, and there is our cosine.

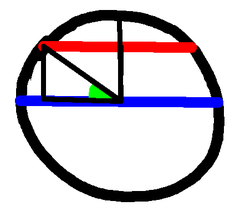
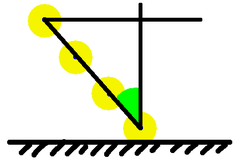
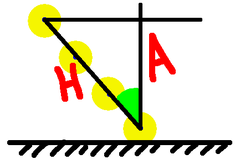
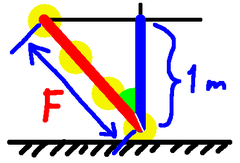
Even better, having chosen the lower point, draw our vertical. Then don't just choose any earlier point on the Sun's path, choose a point that's 1 metre along it. From there draw your horizontal, and the triangle you've produced has a hypotenuse of 1, so the height is the cosine. Now no division is required to get that.

An easier calculation!
So no protractor required after all.

But we can do even better!

Having drawn the Sun's path, mark one point, go up one metre, horizontally over to the Sun's path, and the length of the path so marked is $1/\cos(\theta)$. On our diagram that's the magic factor $F$, and that is the quantity by which we need to multiply our radius measurement.

Update!

It's turns out that the correction is not as simple as just dividing by $\cos(\theta)$, it's more interesting than that.
To see what the the real correction is, have a look on this page: Earth Radius Refined
In other words, we can now multiply these horrible numbers instead of dividing. In these days of the ubiquitous calculator that's not such a big deal, but it does let you do the sums quickly and roughly by hand.

So that's how we can make the correction for latitude using nothing more than the equipment already at hand.

Which is nice.

<<<< Prev <<<<

Just Give Me The Answer

>>>> Next >>>>

Elementary Estimates ...