
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
2019/01/01 - The size of the Earth, a correction.Recently I've been discussing the details of measuring the size of the Earth by watching a shadow descending a wall at sunrise, or ascending at sunset. The sums are easy enough if you do it at either Equinox, and at the Equator, and you can read about it here:
Some work will show that the correction is to divide by the cosine of the latitude, so that's not too hard. But we do (obviously) need to know our latitude.
Well, we're doing all this at Equinox, and at Equinox the angle from the vertical of the Sun's descent or ascent is your latitude. So we can set up a pinhole to cast an image of the Sun on our convenient wall, and measure the angle of its path from the vertical, and there is our latitude.
Hmm. Ah, no, I don't need a protractor.
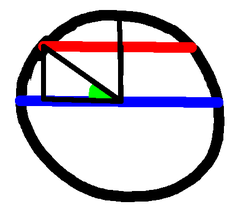
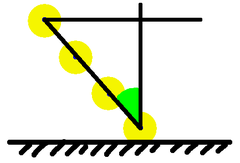
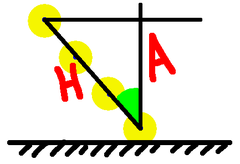
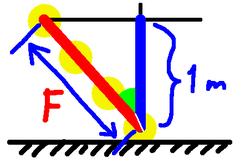
Even better, having chosen the lower point, draw our vertical. Then don't just choose any earlier point on the Sun's path, choose a point that's 1 metre along it. From there draw your horizontal, and the triangle you've produced has a hypotenuse of 1, so the height is the cosine. Now no division is required to get that.
But we can do even better! Having drawn the Sun's path, mark one point, go up one metre, horizontally over to the Sun's path, and the length of the path so marked is $1/\cos(\theta)$. On our diagram that's the magic factor $F$, and that is the quantity by which we need to multiply our radius measurement.
So that's how we can make the correction for latitude using nothing more than the equipment already at hand. Which is nice.
Send us a comment ...
|


 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email