
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
I'm giving a talk for the Liverpool Maths Club this Saturday, April
27th, 2019. I do this roughly twice a year, and it's always a real
challenge - the ages range between 13 and 18, and while some of the
students have been coming for years, for others it might be their
first time. So whatever the topic might be, it needs to be engaging,
accessible, and challenging, all at the same time.
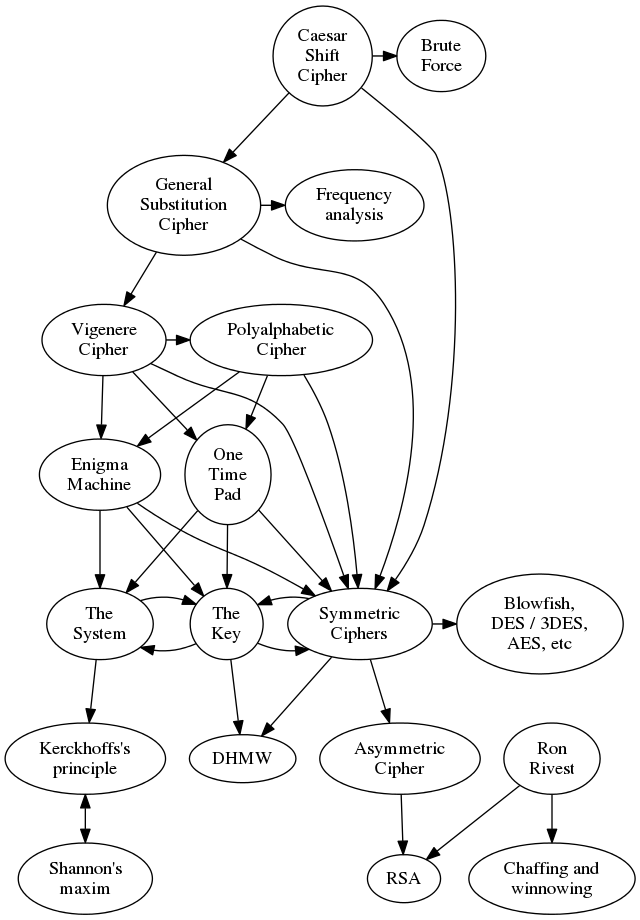
Interesting. But a while ago David Bedford observed that pretty much all talks on cryptography followed the same track. They'd mention steganography, and the story about tattooing the message on a slave's scalp, then they would move quickly to the Caesar Shift Cipher, the Substitution Cipher and how to break it using frequency analysis, possibly mention some subset of the Vigenére cipher and other Polyalphabetic Ciphers, move on to Enigma, mention that "Maths was used to Break Enigma", and finish with:
So David created a talk that briefly mentioned that arc, then picked up where the others finish. In particular, he gave the details of the RSA cryptosystem, how and why it depends on the difficulty of factoring integers, and showed one of the intermediate factoring algorithms, the Pollard Rho method of factoring. Interesting. Picking up on that theme, I've decided to do something similar. I'll also talk about the traditional arc of talks on cryptography, but then emphasise the Shannon Maxim: "The enemy knows the system". From that we can deduce that the system needs to be secure, but the key needs to be secret. To try to plan this I'm putting together diagrams of the topics to help guide me in my design, and to help the students keep track of where we are in the huge network of ideas. Firstly, connections between the different cryptosystems:
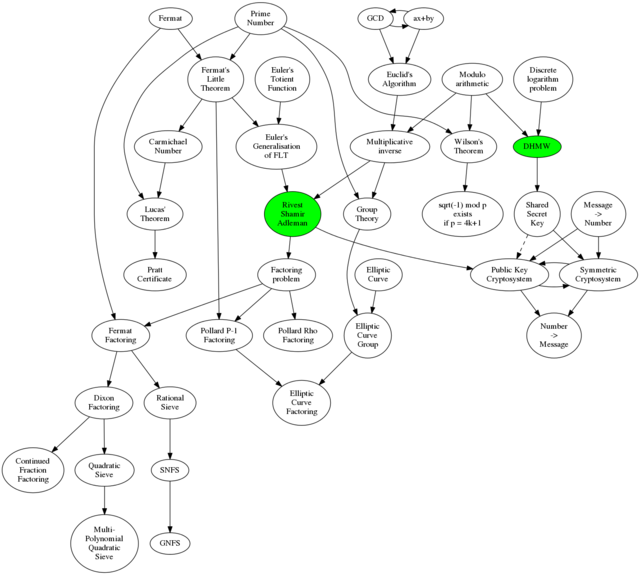
The idea is to cover the idea behind each and the connections between them, but without going into too much detail. The primary purpose of doing that is to get to Kerckhoffs's principle, which is all about the need to separate the concept of the system from the concept of the key. That lets us talk about the challenges of distributing keys, and then of keeping them safe. We can talk a little about couriers in WW2, and how the Enigma operators kept a bucket of water in which to douse the book containing the settings for the month, which was written in water soluble ink. Then we can cover how Diffie-Hellman-Merkle-Williamson (or DHMW) is a miracle - that we can, on an insecure channel, somehow magically agree a shared secret key. Without the background given here we could cover what DHMW is and does, but the "Wow!" factor would most likely be lost. Depending on time and interest I'll also have this diagram showing the connections between the bits of mathematics:
Full size version here: I'll also talk about the pitfalls of implementing your own crypto, so I hope to get the message across that this is suitable for study, but not suitable for implementation without a lot of extra work. We'll see what happens.
Send us a comment ...
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email