
My lastest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Decision Trees in Games (Part 2) - 2011/05/18
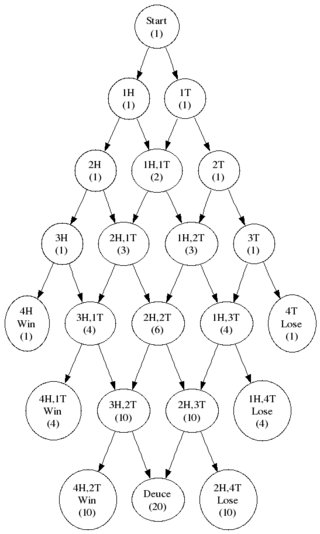
So we start drawing our tree of possibilities, then we realise it will be too big and we collapse it into a DAG, and then we get the situation shown at right. I've marked each node with the score at that node and the number of ways of getting there. In case you're wondering, the number of ways of getting to a node is simply the sum of all the ways of getting to its parents. Some people find that obvious, others don't. So we can see that "H" wins with loads of possible combinations, and we can add them all up. Using D for the probability of winning from Deuce we get:
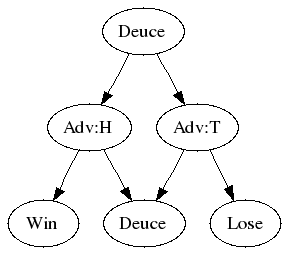
But just what is the probability of winning from Deuce? We can compute the probability of getting to Deuce. Now we just need to compute the chances of winning once we're there. Starting from being Deuce (which is 3 all), let's draw our DAG. We could get two heads, and then we've won, or we could get two tails, and then we've lost. Or we could get one of each (and there are two ways to do that) and we get to 4 all. And here's the clever bit. Our chances of winning from 4 all are the same as winning from 3 all. We must again pull ahead by two, just as we had to do from 3 all. So our chances of winning from 4 all are again D. So our chance of winning from 3:3 is the chance of getting HH, plus twice the chance of winning from 4:4. Thus our chances of winning from 3:3 are p2+2pqD. And that's D. So we have the equation: D=p2+2pqD. We can rearrange that, and we get D-2pqD=p2, and then D(1-2pq)=p2, and so finally we have D=p2/(1-2pq). It's worth checking what happens when p=0, p=1/2 and p=1. That lets us check our answer. So now we get our final expression for the probability of winning a game of tennis. It's this:
It looks complex, but we can see where all the terms come from, and we've been able to sneak up on it. It's not that bad. In my next post, however, we'll find that this hides within it a rather surprising and slightly disturbing result.
Commentsblog comments powered by Disqus
|
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email