Random Physics Question |
|
|
So, is there anyone out there for whom this is easy/obvious?
Thanks.
I'm looking for an expression for the deflection of light in a strong, static gravitational field.
Referring to 'deflection of star light past the sun' in Sean Carroll's "Spacetime and Geometry" - equation 7.80 for the "transverse gradient":
$\nabla\perp\Phi = \frac{GM}{(b^2 + x^2)^{3/2}}\vec b$
 |
$\alpha = {2GMb} \int {\frac{dx}{(b^2 + x^2)^{3/2}}} = \frac{4GM}{b}$
This is only valid for weak fields/small deflection. And I'm not looking for a general integral solution - I'd like to plot photon paths in strong fields, so I'm looking for the instantaneous deflection, which I'll plot/integrate numerically, based on mass, radial distance from mass, and angle of photon trajectory.
It should not use Schwarzschild coordinates, because I don't want the singularity at r=Rs and it only needs to be in 2 dimensions, because of spherical symmetry.
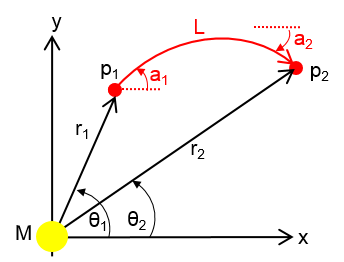
So, is there an expression for the polar coordinates $r_2,$ $\theta_2$ and trajectory $a_2,$ for a photon travelling from $p_1$ to $p_2,$ using $M,$ $r_1,$ $\theta_1,$ $a_1,$ $L$?
$L$ can be small (1/c ?)
Contents |
Links on this page |
|
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email|
|
Quotation from Tim Berners-Lee |
|