It's all too common to try a few examples, find a pattern, try a few more examples, see that the pattern continues, and then leap to the conclusion that the pattern continues forever.

Beware!

This talk gives some examples of patterns that look solid, but which fail, often spectacularly. It goes on to explore the notion of proof in mathematics, and why there are times when we need to be certain.

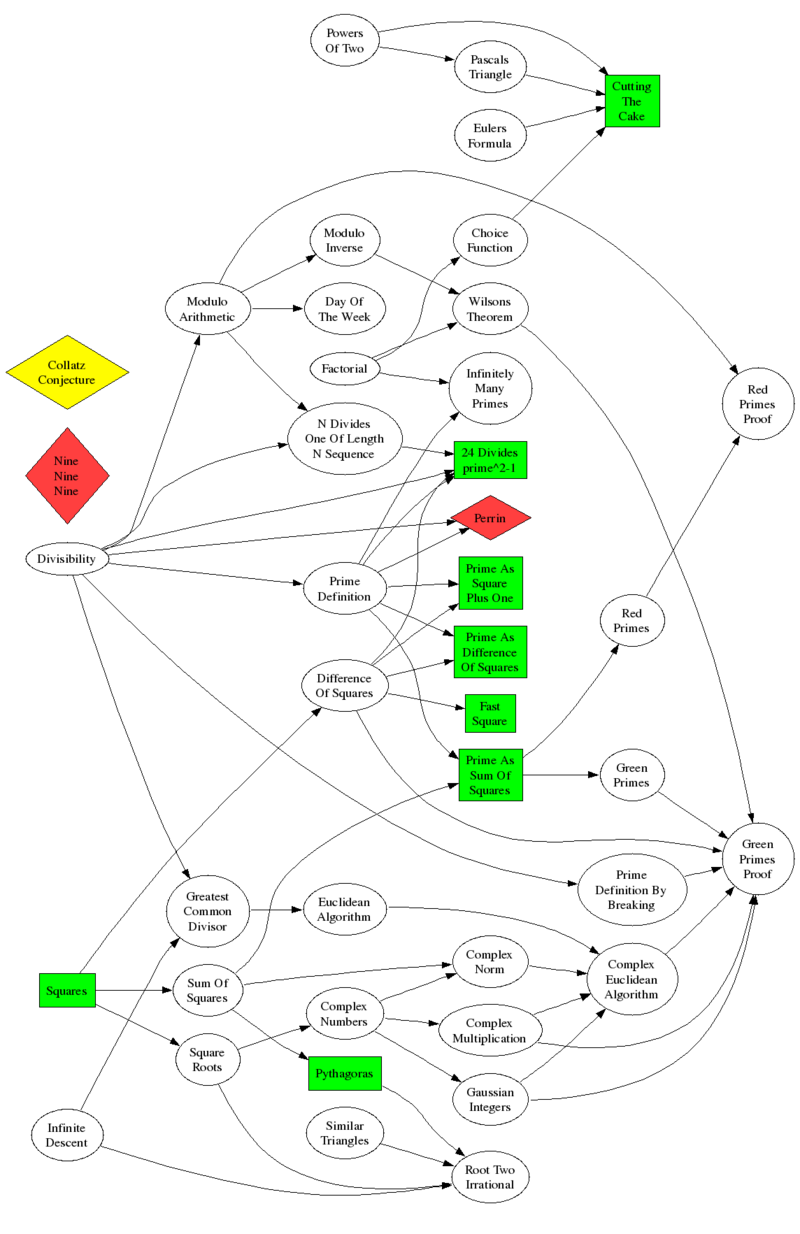
Shown here at right are some of the concepts that might be covered. I say "might" because there is too much to cover in a single lecture/presentation, so parts are left out, parts are glossed over, and there are some things that are mentioned that aren't on the diagram.

The boxes in green are the concepts that are pretty easy to explain without any additional ideas. For example, consider $5^2-1$ and $7^2-1.$ The number 24 is prominent, so try $9^2-1.$ Hmm. What about $11^2-1?$ Ah, there's 24 again. And in $13^2-1,$ but not $15^2-1.$ Again in $17^2-1$ and $19^2-1,$ but not $21^2-1.$ We form the idea that for any prime $p,$ $p^2-1$ is divisible by 24.

Does this always work?

What about expressing a prime as a square plus 1. Can you do that? Can you do it again?

And so forth.

The arrows on the diagram indicate dependencies. We need to know what a prime is before talking about a prime being the sum of two squares, but we need to talk about divisibility to define primes.

A couple of explanations:

• A prime that cannot be expressed as the sum of two squares is called a Red Prime
  • Theorem: An odd prime of the form 4k+3 is red
    • Proof is easy - consider everything module 4.

• A prime that can be expressed as the sum of two squares is called a Green Prime
  • Theorem: An odd prime of the form 4k+1 is green
    • Proof is hard - look at the dependencies.

• "Cutting the Cake" refers to this problem:
  • Put N points on a circle, and join all of them with straight lines
  • How many pieces does this cut the circle into?
    • See Patterns Fail for (a little) more about that

• The proof of root 2 being irrational is a geometric one, not the usual algebraic one

• "Prime Definition By Breaking" refers to this:
  • A number p is prime iff (p|ab => p|a or p|b)

Quotation from Tim Berners-Lee