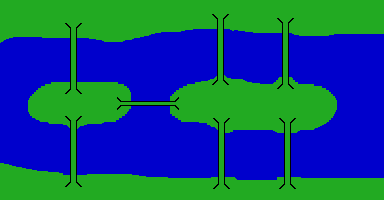
In the town of Koenigsberg there was a river with two islands and seven bridges.
Each Sunday people would go for a walk. After a while someone
noticed that no matter where they started they were never able
to cross each bridge once and only once during their walk. It
seemed that no matter where they started and where they walked,
they would always end up in the wrong place for crossing that
last bridge.
Try it for yourself.
It was suggested that perhaps it was impossible, but there was
always the nagging doubt that perhaps it was possible and
people simply hadn't (yet!) found how to do it.
Then along came a clever chap called Leonhard Euler (pronounced
"Oiler") who settled the matter once and for all. In doing so
he used the main ideas found in all mathematics:
- Abstraction
- Reasoning
- Generalisation
Abstraction
The first thing that Euler did was to say that several things
didn't matter. The shapes of the islands, the lengths of the
bridges, the distances between the bridges, and so on. He threw
away these irrelevant details and ended up with a much simpler
diagram:
Because walking around on land or islands was irrelevant, he
shrunk each of them to a single point, leaving only the lines
representing the bridges.
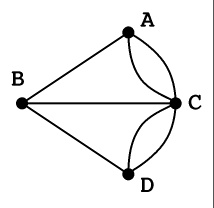
Now observe that if you can draw this diagram without lifting
your pen and without going over any line twice, that gives you
your Sunday walk.
Reasoning
There are four meeting places, here labelled A, B, C and
D, and all of them will have to be visited on our walk. You
might start at one and finish at another, but there will always
be at least two of them that are neither start nor finish. Let's
pick one to think about, we'll call it X.
Since X has some bridges coming to it we will have to visit it
at least once. Since we neither start nor finish there, every
time we come in we must go out again, and on a different bridge.
That means that the total number of bridges that land at X must
be even. For every in there is an out, and if there's an odd
number of bridges, that won't work.
So X, our place that is neither start nor finish, must have an
even number of bridges. However, all our landing places have odd
numbers of bridges,and that makes it impossible to do our walk.
Generalisation
Of course, in the specific case of Koenigsberg it's not that
difficult to try all the possibilities and convince yourself that
it's really not possible. However, the reasoning outlined above
has opened the door to much, much more. We have shown that:
- No diagram can be drawn if it has more than two places
with an odd number of lines.
- If a diagram does have two places with an odd number
of lines, then one of them must be the start and
the other must be the end.
We might wonder:
- Is the opposite is also true? Is it true that if you have
a diagram such that there are no more than two places
with a odd number of lines, then it can always be drawn
without lifting your pen
- This is an example of necessary versus sufficient. We have
shown that it is necessary that at most two places
have an odd number of entry/exit points, but we still
need to show that the condition is sufficient.
- In fact the condition is not sufficient. Can you find
an example?
- Can the reasoning can be adapted to diagrams where the bridges
are one-way, or where only some of the bridge are one-way
- Yes it can, but there are some tricky details to explore
- Instead of asking to cross every bridge, can we find a simple
rule to decide whether it's possible to visit every point
exactly once?
- No-one knows - this is an unsolved problem. In fact, it's
one of the Millennium Problems. If you can solve it, you
can win a million dollars!
This is one of the topics that can be given as a mathematics talk.
Contents
| |
Links on this page
| |
Site hosted by
Colin and
Rachel Wright:
- Maths, Design, Juggling, Computing,
- Embroidery, Proof-reading,
- and other clever stuff.
|
|
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email
Front Page /
All pages by date /
Site overview /
Top of page

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email