
My latest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
The Independence Game - 2017/04/16
It goes like this:
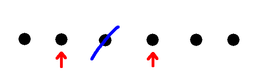
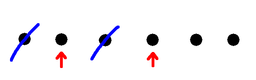
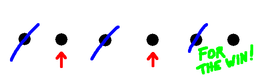
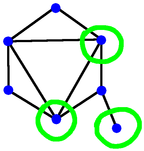
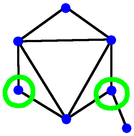
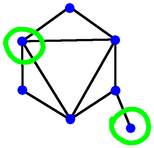
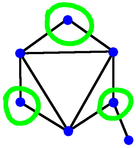
Here at right is an example game with 6 dots. Player 1 takes a dot somewhere in the middle, and that means now neither player can take the dot on either side. Player 2 removes the left-most dot, leaving the two on the far right. Player 1 then wins by taking one of the remaining dots, which also eliminates the other, because it's a neighbour. So in this example game, Player 1 wins. Now suppose we start with an odd number of dots. If Player one marks the middle dot, removing it and its neighbours from the game, we are left with dots on the left, and dots on the right, and no way of interacting. Now no matter what Player 2 does on one side, Player 1 can copy on the other. As a result Player 1 is guaranteed always to have a move, and therefore is guaranteed to win. So with an odd number of dots, Player 1 can always win by marking the middle dot. (There might be other winning moves, but, well, who cares?) So any row with an odd number of dots is a win for the first player. Starting from scratch, a row with just 1 or 2 dots is a win for the first player, because they mark it, and that's the end. A row of 3 dots is a win for the first player if they choose the middle dot. If they are foolish enough to choose an end dot then the second player still has a place to play, takes it, and wins. On the other hand, a row of 4 dots is a win for the second player, I'll leave it to the (mythical) interested reader to work that out, and to work out whether the 6 dot game is a win for the first or second player. So how do we think about this? First digression, a generalisationYou can skip this section if you want to - we're going to do a little Graph Theory. A "Graph" or "Network" is a collection of nodes (also called vertices), some of which are joined by edges (also called lines). Two vertices joined by an edge are called "Adjacent" or "Neighbours". A set S of vertices is called "Independent" if it doesn't contain a pair of adjacent vertices. S is also called "Maximal" if every vertex is either already in the set, or has a neighbour who is. So once you have a maximal independent set of vertices in a graph, you can't add any more.
So we could play a game. Pick a graph, then we take it in turns to pick a vertex to add to an independent set. First one who can't do that wins. Played on a general graph this game is called "Monochrome"[4].
Second digression, the game of NimNow let me introduce you, or perhaps re-introduce you, to the game of Nim. You may have met it before, but bear with me - this is relevant. Very relevant. In Nim we have some heaps of tokens - the heaps need not all be of the same size, and in general, aren't. On each move a player may take any number of items from any single heap, including the option of taking an entire heap. As with the dots game, if you can't make a move, then you lose.
So in the dots game, whenever there are two components of the same size (and more generally, in a game of Monochrome when there are two components that are isomorphic), whatever one player does in one, the other can mimic in the other, and so it's a second player win. Likewise in Nim, if there are two heaps of equal size then the second player can mimic the first player's moves and win. So Nim has some similarities to the Dots game, and perhaps things we learn in the study of Nim can be of use in the study of the Dots game. And indeed, as it happens, both are examples of a more general type of game called an Octal Game[0]. Converting Dots to Heaps.Since Nim is well studied and has lots of cousins, there might be value in thinking of the Dots game somehow as a collection of heaps. We do that as follows. Given that we start with N dots, we think of that as equivalent to a heap with N tokens. When we mark a dot we remove it and any neighbours, and that might leave nothing, one path, or two paths. So:
This exactly falls into the class of Octal Games, and is given the octal encoding of 0.137. It's been studied a great deal, and is equivalent to Dawson's Chess[1], a simplified version of which is called Hexapawn[2], and was written about by Martin Gardner. (This is one of the advantages of having a consistent encoding of games based on what the game is, rather than just a random name that someone made up. Calling the game "0.137" means we can find other games that are, underneath, the same). An analysis of 0.137 ...So we can now look at the octal game 0.137 and see what we can learn. A little notation. We can describe a game position by listing the sizes of the heaps. Further, we can put the sizes in order. So an example position might be (2,4,7). The position with no heaps is (), and is a second person win, because the first player has no moves.
We can also observe that if we have one P position, say (2,2), and another P position, say (4), then the combination of both sets of heaps, in this case (2,2,4), is also a P position. We capture this idea by saying that a P position is "decomposable" or "reducible" if it's a combination of two or more other, non-trivial P positions, otherwise it's "irreducible". So (2,2,4) is reducible. Our challenge now is to find all the irreducible P positions for 0.137 ... A list of P positions ...So we already know that (), (4), and (n,n) for every integer value of n>0 are all P positions. What other P positions are there? If we write a computer program we can quickly check that these are the one-heap P positions up to 100:
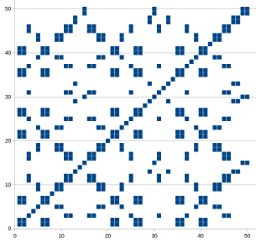
(These are ordered by the total number of tokens). One thing we might ask is whether the density of P positions settles to some sort of limit. From the chart at right here the 2-heap P positions seem fairly uniformly spread. Does that pattern continue? But here is a simple observation. A heap with one token is, as far as game play is concerned, exactly the same as a heap with two tokens. In each case the player would have to take the entire heap. So in this sense, 1=2. That means that every time there is a P position with a 2 in it, we can replace the 2 with a 1. So we can see we have (1,6) and (2,6). We also have (1,7) and (2,7). And then we notice that we also have (6,7). So we start to wonder, if we have (a,b) and (b,c), do we then also have (a,c) ?? Actually, it appears that we do. We have (3,11) and (11,25), and yes, we also have (3,25). We also have (3,3), (11,11), (25,25), and so on. Perhaps we can, in some way, think of 3, 11, and 25 as being equivalent. For example, although I haven't listed the triples here, there is a triple (2,10,17) and we also have (7,10,17). So remembering that (2,7) is a P position, we might hazard the guess that two numbers a and b such that (a,b) is a P position are, in terms of P positions, "equal" or "equivalent" to each other. Looking at the pairings in two-heap P positions we find we get the following equivalence classes:
Yes. Excellent! Let's try another one. Again, let's find a 3 and replace it with (5,6). We look through and find that (3,7,9) is a P position, so we would hope that (5,6,7,9) would also be. But we look through our program output and don't find it. Has it gone wrong? No, it hasn't, because (5,6,7,9) is reducible, being made up of (5,9) and (6,7). So it is a P position, and the idea has in fact worked in this example as well. So whenever we have a triple tuple (a,b,c) it would appear that (a) is equivalent to (b,c), that (b) is equivalent to (a,c), and that (c) is equivalent to (a,b). I wonder if that generalises ... ... and now a miracle occurs.It will, by now, come as no surprise that yes, it generalises. But it not only generalises, it takes us into "This is too good to be true" territory, as a friend of mine calls it. Be warned, this next part takes us into some deep, technical stuff. But it's worth it - the pay-off is huge.
So here is the unbelievable result. In a very real sense, which can be made technically precise:
To understand how all this works we need to make precise the sense in which this game over here somehow corresponds to a single Nim heap, and then we need to work out what that implies. Here's how we start. We are, for each size of heap in Rob's game, going to compute a thing called its "G-value". That's the size of a Nim heap that will, in some sense, be equivalent to the given heap in Rob's game. In Rob's game having no points left to choose is, obviously, a P position. It corresponds to having no heaps left in a game of Nim. So the G-value of () is 0. In each case of a heap of size 1 and a heap of size 2, the only thing you can do is move to (), and that's the same as the situation with a Nim heap of size 1. So the G-value of (1) is 1, as is the G-value of (2). Starting from (3) we can move either to () or (1). So we can get to G-values of 0 or 1, and those are the options for a Nim heap of size 2. So the G-value of (3) is 2. Here we are so far:
So what should the G-value of (4) be? We know it is a P position, so perhaps its G-value should be 0. Yes.
But what about the next position, (5), which has possible destination positions of (2), (3), and (1,1). We know the G-values for the first two of these - 1 and 2 respectively - but what about the G-value of (1,1)?
So the G-value of (1,1) is the XOR of the G-values of the components. The components are both (1), and so each component has G-value 1. So the G-value is 1 XOR 1, which is 0. So our entry for 5 becomes:
The G-value for (5) is 3, being the least value that doesn't appear in the third column. And so we continue:
Looking at these we can list the sizes that all have the same G-value:
Seriously, this looks really good. It is possible to look carefully at moves, Nim, games, sums of games, and derive the concept of the G-value, but those details are for another time. For now we need to take what we've done and see how to use it. How to win at Rob's gameAll of this is very interesting, but ultimately we want to win! So how can we turn this to our advantage? The basic idea is this. Given a configuration, convert all heaps to their G-values, and then XOR them all together. This gives the G-value of the configuration. If the result is 0 then (with perfect play) it doesn't matter what we do, we have lost. It's a P position, and the previous player has won. So what we do is make the position as complex as possible to give our opponent the maximum opportunity for a mistake. But what if the result is non-zero? This is not straight-forward. The easiest thing to specify is simply to look at every possible move, compute the G-value of the result, and choose the one that gives an answer of 0. There will always be one. This process can be simplified, but it's messy. So that just leaves the question of how to compute the G-values. We have a process outlined above - the smallest value that doesn't occur in the list of G-values of positions you can move to - but that's pretty tedious to work out, and it would be nice to have a simpler process. There is. It is a conjecture that for every game of this type, the sequence of G-values of larger and larger components is eventually periodic, and so it proves to be with this one. The G-value of a component of size n is given by:
So here's how to win at Rob's Game.
And so on. But broadly, that's the entire game. Solved. A final example ...
This has a G-value of 5, so there must be a winning move. We try taking an end-point, but g(48)=4, so that's no good. Try taking the second from end, but g(47)=4, so that's also no good. OK, we need to take an interior point. Taking an interior point removes 3 from consideration, so we look at pairs of numbers that add up to 47 and see if we can find two that have the same G-value:
And so we continue. Suppose our opponent takes the middle point of the larger collection, leaving position (6,19,19). What we do is observe that (19,19) is a P position, so if we can convert (6) into a P position, we're set. And we do that by taking an endpoint from the 6, leaving (4), which is a P position. So now we have two P positions, and we play each as a separate game. Whatever our opponent does, we do the right thing in that game, greatly simplifying the calculations we have to perform. AddendumLest you think that everything is sorted, there is a book called "Unsolved problems in combinatorial games" by Richard J Nowakowski[7]. In that, question number 2 asks if all games such as we've been describing are, in fact, periodic. We just don't know. Take a specific example such as the game "Officers", which is 0.6 using the Octal Game notation[0]. We don't know if that's periodic, and as of November 2012, Achim Flammenkamp's list of octal games[8] has explored up to $2^{47}$ positions without a proven solution. We just don't know. So there are still problems to explore, results to be found, papers to be written, and games to be analysed. I hope this has been an interesting introduction to Combinatorial Game Theory[9].
Credits and References:
[0] https://en.wikipedia.org/wiki/Octal_game [1] http://www.di.fc.ul.pt/~jpn/gv/dawsonchess.htm [2] https://en.wikipedia.org/wiki/Hexapawn [3] Mathematical Games, Scientific American, March 1962, reprinted in The Unexpected Hanging and Other Mathematical Diversions, by Martin Gardner, pp. 93ff [4] https://en.wikipedia.org/wiki/Map-coloring_games#Monochrome_and_variants [5] https://en.wikipedia.org/wiki/Octal_game#Game_specification [6] https://en.wikipedia.org/wiki/Sprague-Grundy_theorem [7] http://library.msri.org/books/Book63/files/131106-Nowakowski.pdf [8] http://wwwhomes.uni-bielefeld.de/achim/octal.html [9] https://en.wikipedia.org/wiki/Combinatorial_game_theory
Send us a comment ...
|


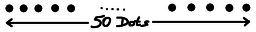
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email