 Subscribe! Subscribe!

My latest posts can be
found here:
Previous blog posts:
Additionally, some earlier writings:
|
2017/10/03 - Four points - the proof
The Four Points Puzzle challenge that Peter Winkler set me was this:
- Find all configurations of four (distinct) points
in the plane that determine exactly two distances.
As I remarked earlier, given four points there are six possible pairs,
so in general, four points in the plane will determine six distances.
But we can choose to place the points to create duplication, and the
challenge here is to find all possible ways to do that and end up with
only two distances.
That's reasonable, and lots of people have sent me their solutions.
Peter had also said:
- "Nearly everyone misses at least one, and for
each possible solution, it's been missed by
at least one person."
So the challenge isn't really to find all the configurations so much
as to be able to prove that you have them all. That's what I'm going
to do here, so if you haven't had a go at the puzzle, now is the time
to bookmark the page, close the browser, get yourself a tea, coffee,
or other beverage of your choice, and have a go.
Remember, it's the proof that matters.
Here's mine.
Preliminaries ...
We have four points, and therefore six pairs. But we only have two
distances, so some are short, and some are long. The short ones are
all the same as each other, and the long ones are all the same as each
other. Obvious, I know, but we're just warming up.
So let's prove a few simple results.
Lemma: No three points are collinear.
(If you're happy with this you can skip the box)
|
These sorts of proofs, descriptions, and discussions can really
stretch your visualisation skills. If you're an experienced mathematician
you'll know that you can't just skim this sort of thing and try to
"Read like a novel" - you need to take pencil/pen and paper and draw
what's going on. And if not literally with pen and paper, then at
least to work on explicitly visualising it.
You need to "Read like maths" - because it is. |
If points $A$, $B$, and $C$ are collinear, with $B$ between $A$ and
$C$, Then $|AC|$ is the long distance, and both $|AB|$ and $|BC|$ are
the short distance. Consider point $D$ ... we have two possibilities.
If $D$ is the same distance from $A$ and $C$ then that must be the
long distance, but then $|BD|$ is neither $|AB|$ nor $|AC|$. So
that doesn't work.
So $|AD|$ and $|CD|$ are different lengths. Up to symmetry we can
compute exactly where $D$ must lie, then observe that again, $|BD|$
is neither of our possible lengths, so that doesn't work either.
So there is nowhere to put point $D$, and hence no three points can
be collinear.
|
Observation: Each edge is in exactly two triangles. (It's worth
taking some time to convince yourself of this)
Lemma: There are at least two short edges that share a vertex.
(Again, if you're happy with this, skip the box)
|
We cannot have no short edges, because then we'd have all long edges,
and the points would have to be in a tetrahedron, which isn't in a
plane.
We cannot have exactly one short edge, because then the other five
would all be long, and have to form two equilateral triangles with a
shared edge. The remaining edge would have to be longer.
So we must have two or more short edges. Any three or more edges
must share at least one vertex, so we only need to worry about the
case where we have exactly two short edges.
We cannot have $|AB|$ and $|CD|$ as the only short edges, because both
$C$ and $D$ would have to be on the perpendicular bisector of the line
$AB$, and they would have to be on opposite sides of the line, making
$|CD|$ too long. So if there are exactly two short edges they must
share a vertex, which is what we need.
So there are (at least) two short edges that share a vertex.
|
Now for the single insight that, I think, makes the enumeration of all
solutions quite straight-forward. The fact is simple, making certain
it is a fact is a little tedious - feel free to skip this section if
you're happy with the statement of the lemma.
Lemma: There is a triangle with two short and one long side.
We proceed by the cases of how many long edges there are.
We cannot have no long edges.
If there is exactly one long edge then either triangle it forms will
suffice.
If there are exactly two long edges, consider one of them. It is part
of exactly two triangles, at most one of which can contain the other
long edge, so at least one of which has two short sides.
If there are exactly three long edges then we have three short edges.
Take two that share a vertex - $AB$ and $BC$. If $AC$ is short then
all distances to $D$ would have to be long, which is not possible.
So $AC$ is long, and $ABC$ is our required triangle.
If there are exactly four long edges then the two short edges share
a vertex and the remaining edge of that implied triangle is long.
We cannot have exactly five or six long edges.
So we are done.
Finding all solutions ...
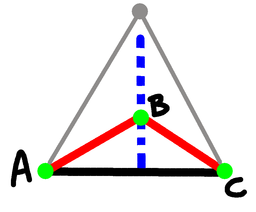
Triangle with
two short sides
|
So now we know that there is at least one triangle with two short
sides and a long side. So let's call that $ABC$ with $AC$ being the
long edge. We can see that $B$ has to be on that blue line, above the
line $AC$, and because the red lines are the shorter ones, $B$ cannot
be as high as the grey point, which forms the equilateral triangle with
$A$ and $C$.
Now let's consider the fourth point, $D$. We can assume that $D$ is on
or to the right of the blue line, because if it isn't, reflect around
that line, and now it is!
The distances from $D$ to each of $A$, $B$, and $C$ must be short or
long, so let's write all the possible combinations of each of those
distances.
| Case |
Distance
to $A$
|
Distance
to $B$
|
Distance
to $C$
|
|
0
|
Short
|
Short
|
Short
|
|
1
|
Short
|
Short
|
Long
|
|
2
|
Short
|
Long
|
Short
|
|
3
|
Short
|
Long
|
Long
|
|
4
|
Long
|
Short
|
Short
|
|
5
|
Long
|
Short
|
Long
|
|
6
|
Long
|
Long
|
Short
|
|
7
|
Long
|
Long
|
Long
|
Cases 1 and 3 are not possible, for then $D$ would be to the left of
the blue line, which we have excluded.
|
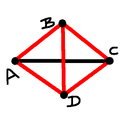
Case 0 (sss): Point $D$ has to be the reflection of point $B$ across the
line $AC$ giving a pair of equilateral triangles that share an edge.
|
|
|
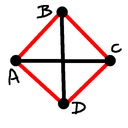
Case 2 (sls): As case 0, point $D$ has to be the reflection of point $B$
across the line $AC$. In this case we get a square with $AC$ and $BD$
as diagonals.
|
|
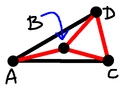
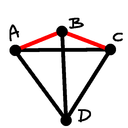
Case 4 (lss): The triangle $BCD$ is equilateral, and $ACD$ is isosceles.
|
|
|
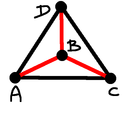
Case 5 (lsl): Here $ACD$ is equilateral, and $B$ is in the middle.
Point $D$ must be where the grey point is on the diagram above.
|
|
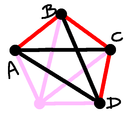
Case 6 (lls): Here $D$ is a little below $C$, and the four points
are the points of a regular pentagon.
|
|
|
Case 7 (lll): Now point $D$ forms an equilateral triangle with $A$
and $C$, and must be the opposite side of the line $AC$ from the point
$B$. The points form a kite.
|
So there are 8 combinations, two of which are impossible, and the other
six give exactly one solution. The only remaining question is whether
any of the options might give more than one possible solution, but that
doesn't happen. In each case the location of point $D$ is completely
determined by the options given, so we're OK.
And we are done.
- Did you get them all?
- Which one (or ones) did you miss?
- Which one did you find last?
- How did you prove that you had them all?
Send me email from the comment box below.
Other solutions ...
Here is the solution from Josh Jordan:
Send us a comment ...
|









 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email