
My lastest posts can be found here: Previous blog posts:
Additionally, some earlier writings: |
Decision Trees in Games (Part 3) - 2011/05/24
where D is the probability of winning from Deuce and is given by:
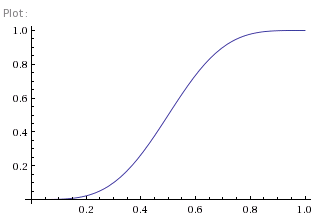
Figure 1 shows a graph of this. Graphs curtesy of Wolfram Alpha:
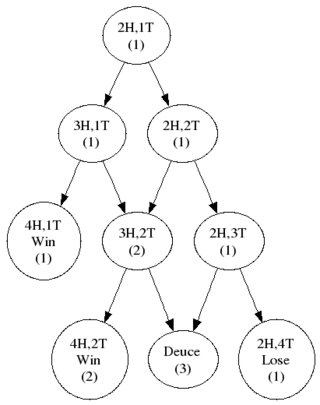
It's interesting to see that once your chances of winning each point gets above 80% you're pretty much certain to win the game, and increasing the per-point percentage is pretty much, well, pointless (if you see what I mean). So that's interesting, but hardly surprising. Using exactly the same techniques we can now compute how our chances change through a game. Suppose, for example, we win two points and lose another, so we are 30:15 up. We're ahead, we're winning, so you'd suppose our chances of winning the game have increased. Figure 2 shows the decision tree (well, graph) and so we can compute our chances of winning are now:
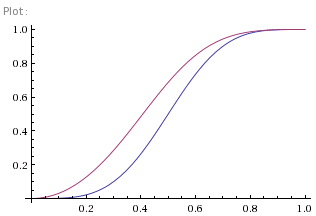
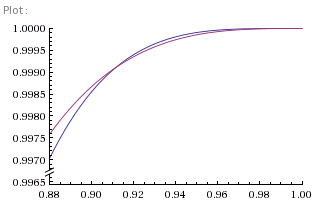
where, as before, D is the probability of winning from Deuce. Figure 3 shows this new probability in red, and, as we can see, it has gone up, just as expected. No, but wait! Let's have a closer look at the high percentage portion of the graph. Figure 4 shows a close up view of the section where our chances of winning each point are around 90% or more, and there's something of a surprise. Our chances of winning, even though we're already ahead, have actually gone down. How can that be true? It's hard to be convincing about this without resorting to the equations. However, one intuitive way of thinking about it is this. When your chances of winning each point are so large, more than 90%, the chances of losing a single point are small. So small, in fact, that losing a single point in the game is enough to swing the chances of the whole game against you. Not wholesale, obviously, since you're still overwhelmingly likely to win the game, but by some. Having two points is almost irrelevant - it's to be expected. So being 30:15 up in the game actually is a bad thing, because you've lost a point you were expected to win. The cross-over happens at (1+√7)/4 which a shade over 91.1% as the graph shows. And that's the other slightly unexpected thing. If your chances of winning each point independently are less than 90%, the cross-over doesn't happen, because losing a point isn't sufficiently surprising. Which I find slightly surprising.
Commentsblog comments powered by Disqus
|

 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email