Cycloid

|
AllPages RecentChanges Links to this page Edit this page Search Entry portal |
|
|
|
Cycloid |
|
||||
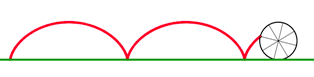
An animation of the generation of a cycloid can be found at http://mathworld.wolfram.com/Cycloid.html
The parametric equations of a cycloid passing through the origin generated by a circle of radius a in Cartesian coordinates are
The cycloid is the solution of the Brachistochrone Problem - Find the shape of the curve in which a wire must be made so that a bead will slide freely under gravity from one point to another in the same vertical plane in the shortest time.
Therefore, if a ski resort wanted to get skiers from the top to the bottom of a mountain in the shortest time, the mountain should carved out into the shape of a cycloid.
http://en.wikipedia.org/wiki/Brachistochrone_problem
The cycloid is also the solution of the Tautochrone problem - Find the shape of the curve in which a wire must be made so that the time taken by a bead sliding without friction under gravity to its lowest point is independent of its starting point.
A pendulum does not keep perfect time if the amplitude (angle) of swing changes. However if a bead is allowed to swing on a frictionless wire in the shape of a cycloid it will keep the same time whatever the size of the oscillation.
Christian Huygens was able to use this property of the cycloid to make an improvement to the simple pendulum clock.
http://en.wikipedia.org/wiki/Tautochrone_curve