Axiom
AllPages
RecentChanges
Links to this page
Edit this page
Search
Entry portal
Advice For New Users
An axiom (or postulate) is any mathematical statement that is the starting point from which other statements (often called theorems) are logically derived.

Axioms are considered self-evident requiring neither proof nor justification.

Many areas of mathematics are based on axioms: set theory, geometry, number theory, probability, etc.

At the start of 20th Century Mathematicians showed great confidence in the development of the axiomatic foundations of Mathematics. However this confidence was shattered by the work of Kurt Godel.

One requirement of an axiomatic system is that it is consistent i.e. does not lead to contradictory theorems - thus creating a paradox (see Russell's Paradox).

Here are the axioms of Euclidean Geometry

  • Any two points can be joined by a straight line.
  • Any straight line segment can be extended indefinitely in a straight line.
  • Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as centre.
  • All right angles are congruent.
  • If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.

From these, all the rich and interesting theorems of school geometry can be derived.
It is possible to have different and conflicting axiomatic systems which lead to consistent but different areas of Mathematical study.

In Euclidian Geometry the 5th (or parallel) postulate states:

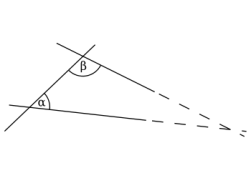
However Nikolai Lobachevsky (1792 - 1856) and János Bolyai (1802 - 1860) considered this axiom was not self-evident. When they investigated the effect of substituting an alternative axiom such that lines do not meet, however far extended, found no resulting contradictions thus formulating the first non-Euclidian Geometry. This Geometry (called hyperbolic geometry) has many features different from Euclidean Geometry. For example, the sum of the angles of a triangle is less than 180 degrees and the greater the area of the triangle the smaller the sum. Poincare's Disc is a model of such a geometry.

Different axioms lead to different geometries. Mathematics thus supplies a number of competing descriptions of Space, the correct interpretation being found experimentally. The descriptions of Space by Albert Einstein and others requires Space to be non-Euclidean.

Links to this page / Page history / Last change to this page
Recent changes / Edit this page (with sufficient authority)
All pages / Search / Change password / Logout