TheAlgebraicPentagon

Created Monday 11 August 2025

A note to readers ...


This is a hurried write-up of a talk I gave some months ago. It was
aimed at a specific audience and this write-up reflects that, but I'm
interested enhancing it to appeal to a wider audience.

So I'm interested in any and all feedback. If I don't agree then I'll say
so and we might have a discussion, and if I do agree then you will
have helped enhance the piece.

Feedback channels at the end.

Published under CC BY-NC-ND:


The Algebraic Pentagon


As a child I spent far too much time playing with a compass and ruler.
I drew all sorts of things from mathematical shapes to complex road
junctions. I could draw perfect triangles, perfect hexagons, perfect
squares, and when I learned how to bisect a line segment I could then
double up the sides and draw perfect octagons, and so on.

So I could draw:

But ... what about the missing shapes? Is it possible to draw those
using just a compass and an unmarked straight-edge? In particular,
can we draw a perfect pentagon with just a compass and straight-edge?

This question of constructing a pentagon was, in fact, settled by Euclid
in around 300 BC, but the more general question had to wait. I'm in
the process of getting precise references, but certainly Gauss solved at
least some of it, and Pierre Wantzel (1814-1848) may or may not have
contributed more. More work to do with regards the exact history and
attribution.

These days we can easily look up a method for constructing a regular
pentagon. There are dozens, if not more. But the question remains:

How do you know it's right? How do you know it's perfect?

So let's create for ourselves a compass and straight-edge construction
of a regular pentagon.

We begin with a detour into some simple arithmetic viewed in a rather
strange way.

Stretching the number line


Let's have a look at our old friend, the number line:


We are accustomed to thinking about multiplication of positive integers
as "Taking Multiple Copies", but instead, let's think about stretching
the entire number line. Let's stretch it by a factor of 2:


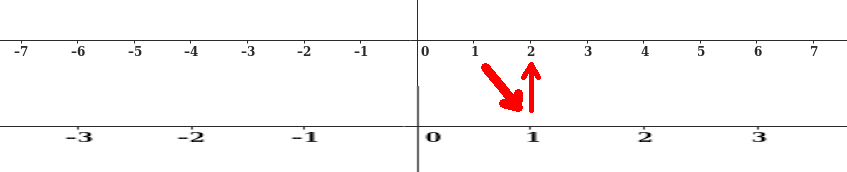
We can see that the line has been stretched by 2 because we see where
the number 1 has ended up. The number 1 has ended up in location "2",
so it has been stretched by 2.

Now stretch again, this time by 3:

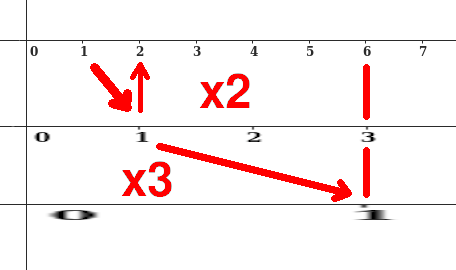
(Figure 2b)

The final result has the number "1" now in location "6". The net
result of stretching by 2, then stretching by 3, is that we have
stretched by 6. So we can thinking of multiplication not as taking
multiple copies, but instead as successive transformations of the
entire number line. In this way we do *not* get "for free" that
A times B is the same as B times A, but as we shall see shortly,
there are other benefits.

Now if I say that I have stretched the number line by some amount,
and then stretched it again by the same amount, can you tell me by
how much I stretched it each time? What if the number "1" has
ended up in location "49" ... how much did I stretch the line?

It's not hard to verify that a stretch by 7, applied twice, will
leave "1" in location "49". Working out what has been done twice
to create a final result is what we call taking the square root
of a number (or more generally, of an operation).

The square root of a number "N" is the transformation we need to
apply twice to have "1" end up in location "N".

Now ... what is "Multiply by -1"?

If we take the number line and swap it end-for-end, the number "1"
ends up in location "-1", so that is the transformation of the line
corresponding to "Multiply by -1". We swap the line, end-for-end.

So far, so good.

Now ask:

What transformation can we apply to the number line twice to have
"1" end up in location "-1"?

Some people see this instantly, others take a while, but when you
see it, it's lovely.

Rotate the line by 90 degrees.

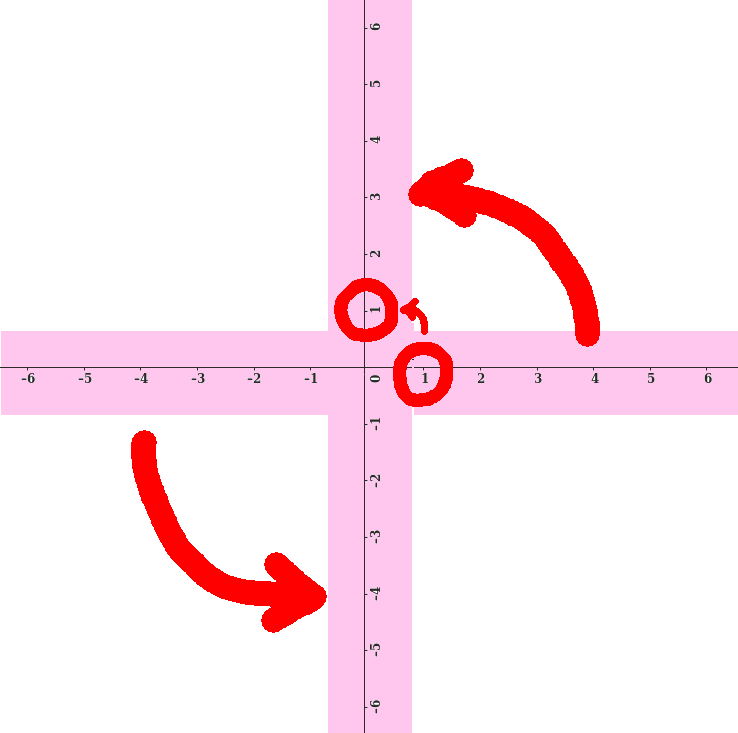
(Figure 3)

Do that twice and "1" ends up in location "-1", so the square root
of "-1" is the operation of rotating the number line by a quarter
turn.

But what have we "multiplied by"? Where has "1" gone to?

We can see that "1" has gone "off the line" and is now hovering
somewhere "out there". We can give a name to this location, but
the more important thing is that this location can be thought of
as a number, and multiplying by that number rotates things by a
quarter turn.

So this location out here is, in a very real sense, the square
root of minus one. If we add one to that it's the same as taking
a step to the right. Subtracting one is a step to the left.
Multiplying by 2 is now expanding the entire plane by a factor of
2, and so on. We get all our arithmetic operations acting on the
entire plane, so we call it "The Complex Plane".

From here on we will be making reckless use of the connection
between "numbers" and "transformations" and "coordinates". For
any given "thing", sometimes we will think of it as a number in
its own right, sometimes we will think of it as a location on the
plane, and sometimes we will think of it as a transformation to
be performed. Yes, we will be leaping about without justifying
fully the connections we make, but this isn't an article about
complex analysis, this is an example of seeing it in action.

So the X-Axis is the collection of "Real Numbers", the Y-Axis is
the X-Axis rotated by a quarter turn, and we will slip freely
between these ways of thinking about them.

But now let's look at a special operation, and a special point.

Rotated by one fifth


Let's start with our plane, and I want to think of rotating it
(anticlockwise) by a fifth of a turn. As we've seen, rotating
things can be thought of as "multiplying by some number", so
exactly what number does a "fifth of a turn" correspond to?

To answer that we do what we did before, and ask: Where does
the "1" go?

Well that's easy, it goes one fifth of the way around the circle
of radius 1, so it goes here:

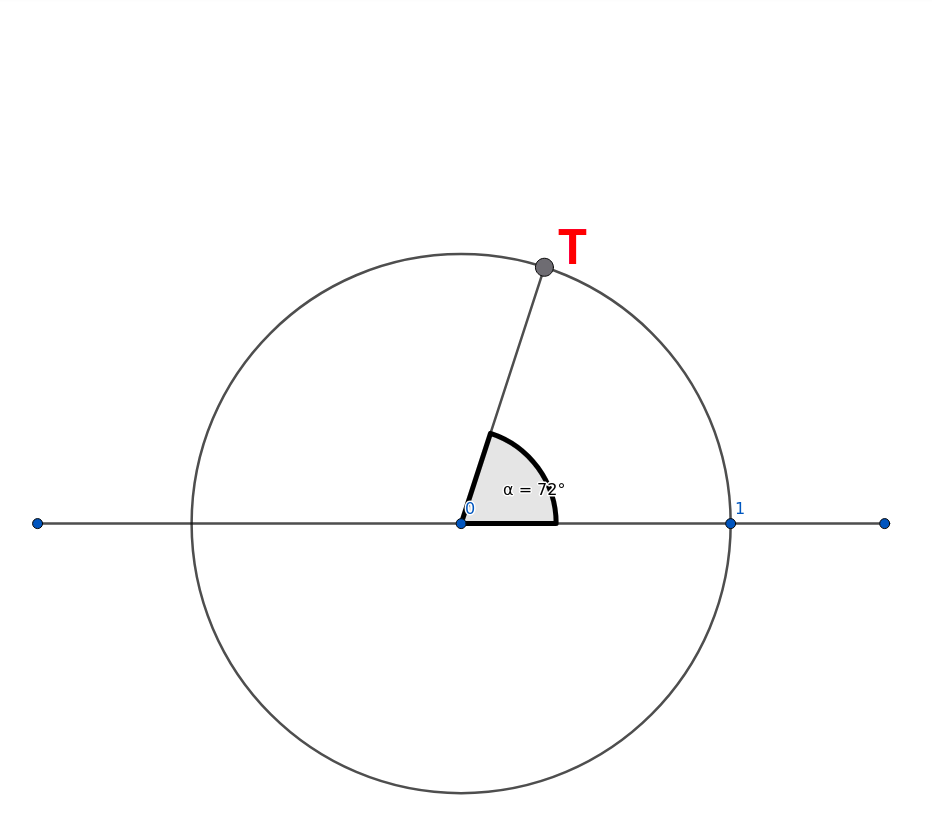
(Figure 4)

Let's call this point "T". So rotating the plane by one fifth is
"Multiplying by T". We can think of "T" as a point on the plane,
but we can also think of it as a thing to multiply by. It is, in a
very real sense, a number.

So if we do that again, multiply by T again, then now "1" has been
taken two fifths of the way round the cicle. And again, and again,
and again, and with five multiplications by T, our point "1" is back
where it started.

So we start with "1", and multiply by "T" five times, and we have:

Or T5 = 1.

And we are into algebra! In a very real sense we would now like
to solve the equation: x5-1=0. If we think of the solutions of
that equation (and there will be more than one solution) as being
like points in the plane, then one of them is our point "T". But
via algebra we can show that if "T" is a solution to x5-1=0 then
so are T2, T3, and T4. These are all rotations of each other
by a fifth of a circle.

These will form the vertices of a regular pentagon!

So if we can find solutions to the equation x5-1=0 we can find
the vertices of our regular pentagon. So let's do that.


Solving x^{5}-1=0


We can start by observing that x=1 is a solution, and that means
(via the remainder theorem) that x5-1 is exactly divisible by (x-1).
So we divide that out and we get this:

x5 -1 = (x-1)(x4 + x3 + x2 + x + 1)

So we are looking for solutions to that quartic.

(You can skip this next paragraph)

We know from the geometry that the solutions will come in pairs,
and those pairs will be complex conjugates. That, in turn, means
that those pairs will be solutions to quadratics, and putting all
that together means we can factor the quartic into the product of
two quadratics.

So we have this:

(x4 + x3 + x2 + x1 + 1) = (x2 + ax + 1)(x2 + bx + 1)

Symmetry is our friend here, and using it we can deduce that the
leading terms and constant terms must all be 1. Expanding and
equating coefficients we have:

a+b = 1 (*)

and

2+ab = 1, or ab = -1

Using (*) we can write b=1-a. Substitute and rearrange and we
have this:

a2-a-1 = 0

Being a quadratic, this will have two solutions, and by symmetry
(our friend again!) we can have one of them as "a", and the other
as "b". Now we can use our other friend, the quadratic formula,
and we find the solutions:

a = (1 + sqrt(5))/2

b = (1 - sqrt(5))/2

We have found the Golden Ratio! This is wonderful, because the
Golden Ratio turns up all over the regular pentagon ... we must
be on the right track! (If you don't know the Golden Ratio then
don't panic, but the genuine maths behind it is fabulous and is
connected to Fibonacci and all sorts of things. Just avoid all
the pseudo-maths that has ... regrettably ... arisen around it).

Now remember, we are trying to find solutions to x5-1=0. Those
are x=1, and the solutions to:

x2 + ax + 1 = 0

and

x2 + bx + 1 = 0

Concentrating on the first of these, we know that "a" is the
Golden Ratio, so we are trying to solve:

x2 + φx + 1 = 0

Using the quadratic formula again we can solve that, and we get:

x = ½(-φ + sqrt(φ2-4))

But wait! There's more!

The points we want are on the unit circle, so really it will be
enough to find the real part of this solution. If we can find
that point on the real line, we can construct perpendiculars up
to and down to the circle, and we get the points we want!

So all we need is:

Re(x) = -½φ

Which is: -1/4 - sqrt(5)/4

Working through the algebra with "b" instead of "a", we use "-1/φ"
instead of "φ", and we get the other point of interest:

Re(x) = -1/4 + sqrt(5)/4

The payoff ...


Let's see this emerge in a construction, and let's try to do it
"efficiently" in terms of the number of steps we make. (In truth
this isn't the most efficient, but it does arise directly from
the algebra.)

Start with a line, which we are going to think of as the so-called
"Real Numbers."

Mark a point that will be our centre. This is going to be "Zero".
Set the compass to some suitable size, and draw a circle. That
will cut the line in two places, which we will call "-1" and "1".

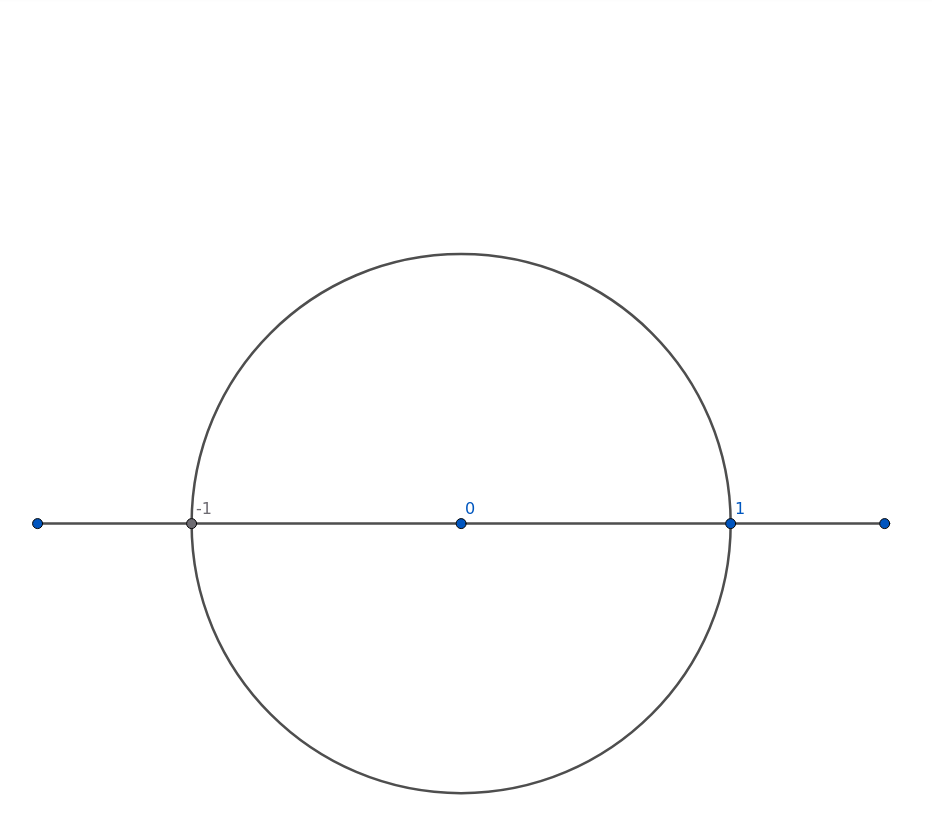
(Figure 5)

Keeping the compass at the same setting, put the point at "-1"
and mark the circle above and below. Call these points "A" and
"B". Join these with a straight line to find the point -1/2 on
the line.

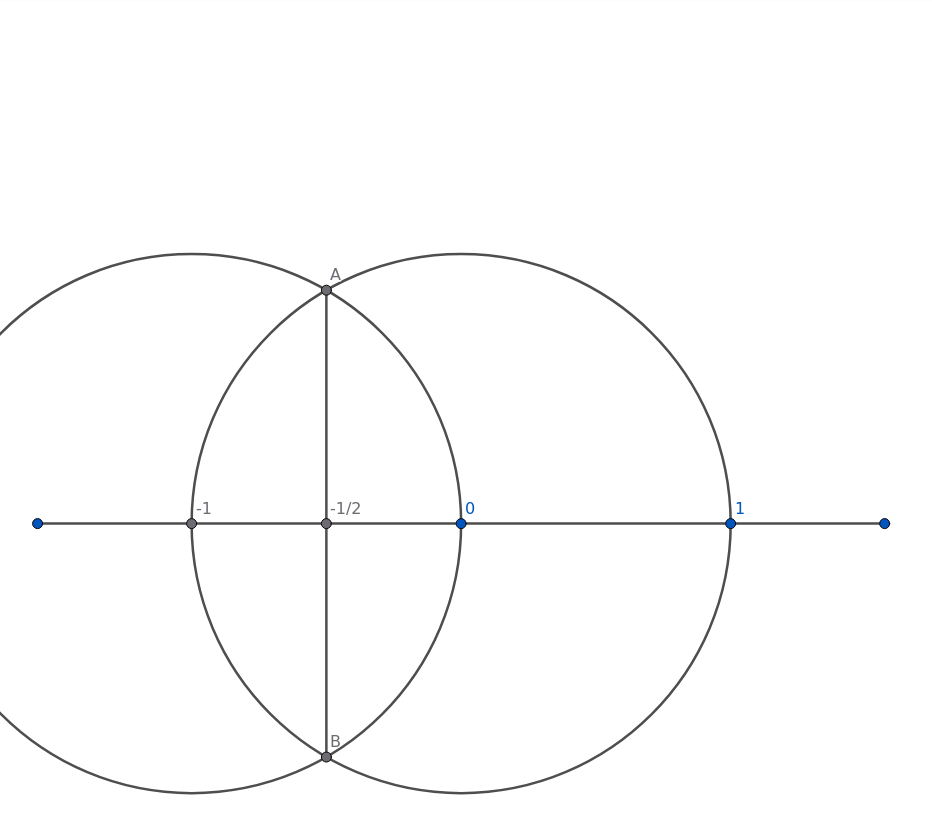
(Figure 6)

Still with the same setting, put the compass point at "1" and
going anti-clockwise, mark the unit circle at a point we shall
call "C". From each of A and C draw arcs above the circle. We
will call the point where they meet "D". Connect "D" to "O".
This intersects the unit circle at the square root of -1.

In other words, at "i".

The line from "D" to "O" is at right angles to our initial line,
which you will recall is the line of "Real Numbers".

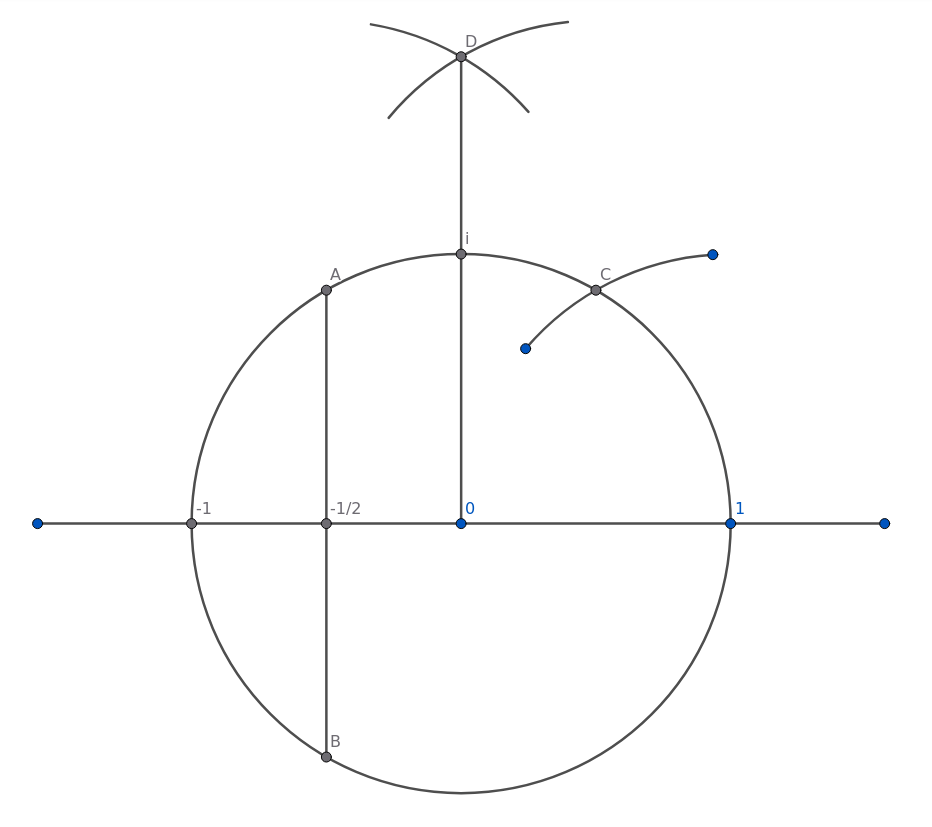
(Figure 7)

Again keeping the compass at the same setting, put the compass
point at "i" and draw the arc cutting the unit circle on the
left at "L" and on the right at "R". Join these to cut the
vertical line at "½".

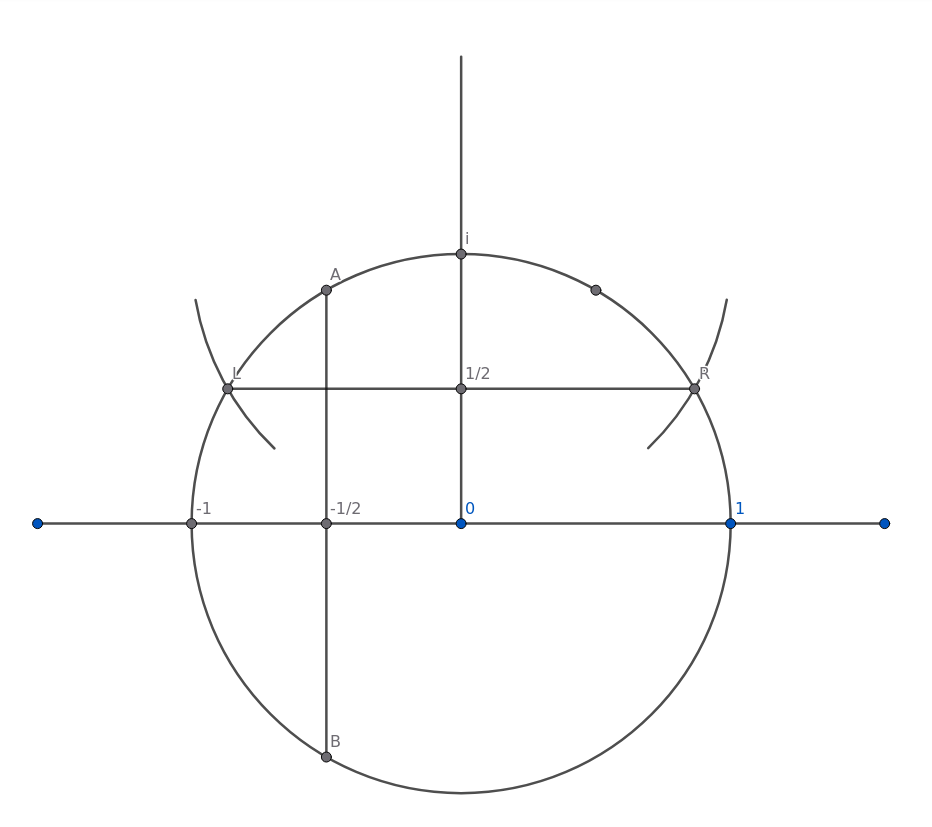
(Figure 8)

And yet again keeping the compass at the same setting, put the
point on the X-Axis at -½ and cut the unit circle at A' above
and B' below. Join these and we have constructed -¼.

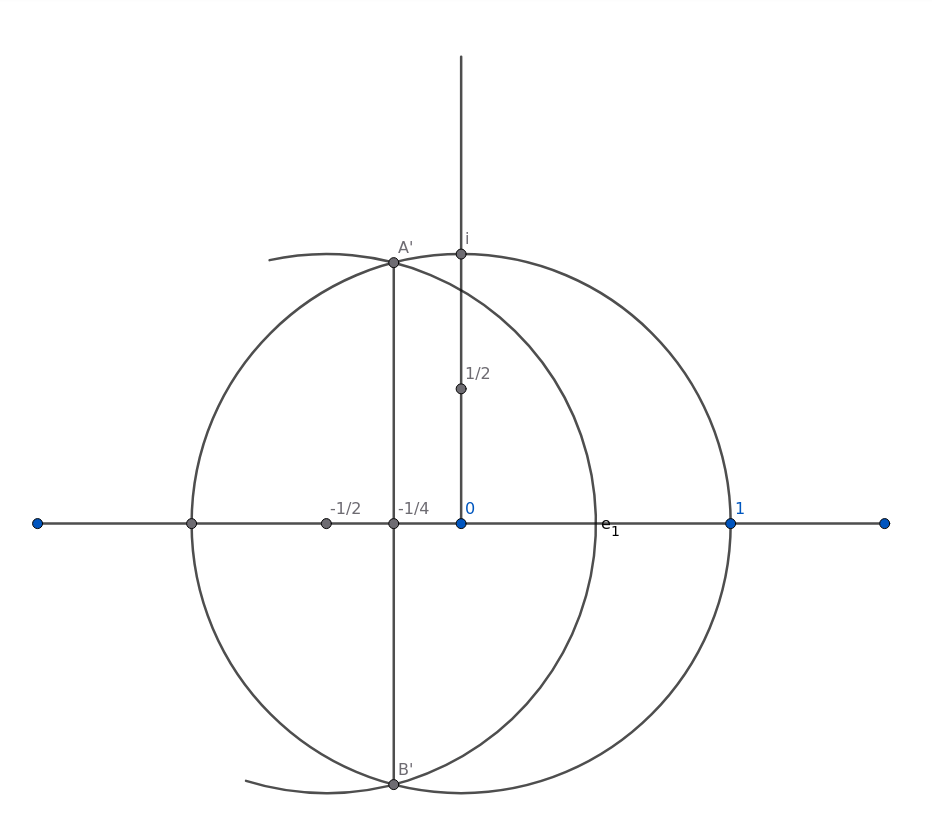
(Figure 9)

Now pause.

Our objective is to construct these two points on the X-Axis:

U = -1/4 - sqrt(5)/4

and

V = -1/4 + sqrt(5)/4

Thinking in terms of coordinates, we have constructed:

(-¼,0) ... a quarter step leftwards from the centre

and

(0,½) ... half a step upwards from the centre

By Pythagoras (he just had to get mixed up in this!), the
distance between those two points is:

sqrt(5)/4

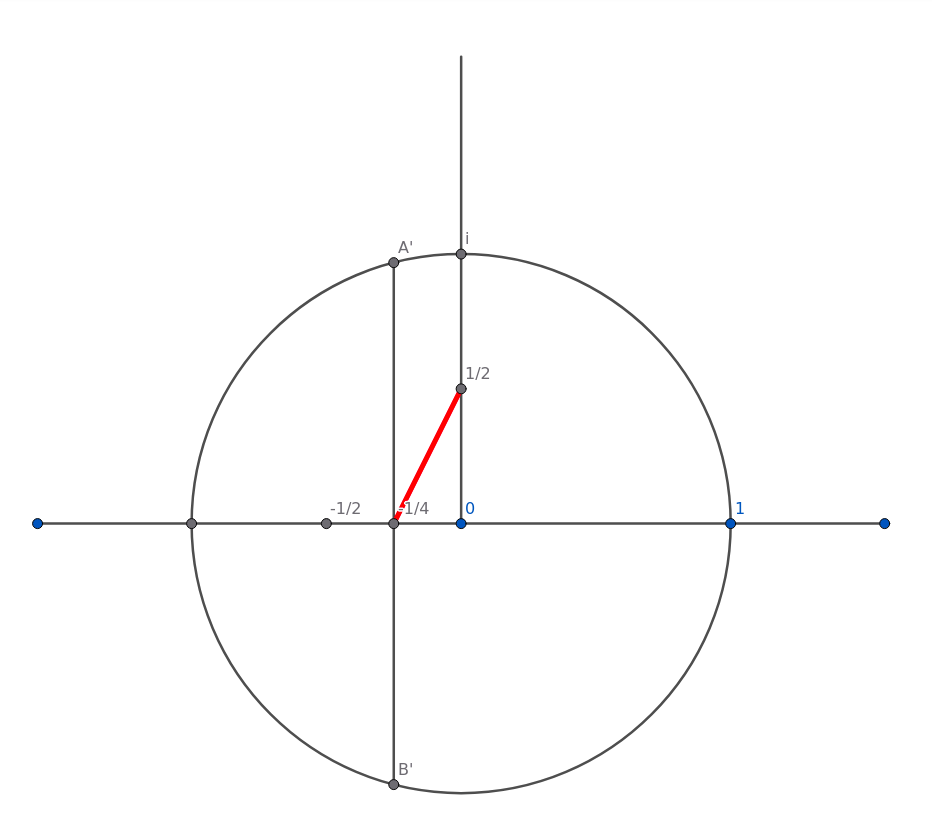
(Figure 10)

So ...

For the first time we change the setting on the compass. Put
the point on (0,-¼) and the pencil on (0,½). The distance is
now sqrt(5)/4, so we can swing that around, and where it cuts
the X-Axis we have found these points:

U = -1/4 - sqrt(5)/4

and

V = -1/4 + sqrt(5)/4

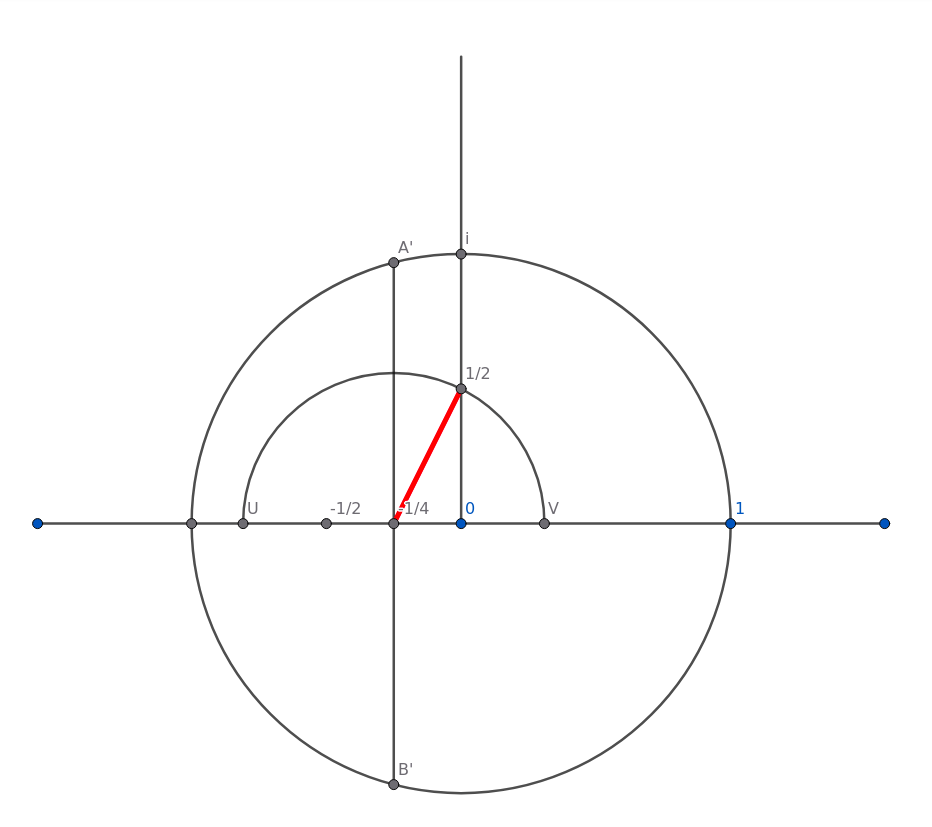
(Figure 11)

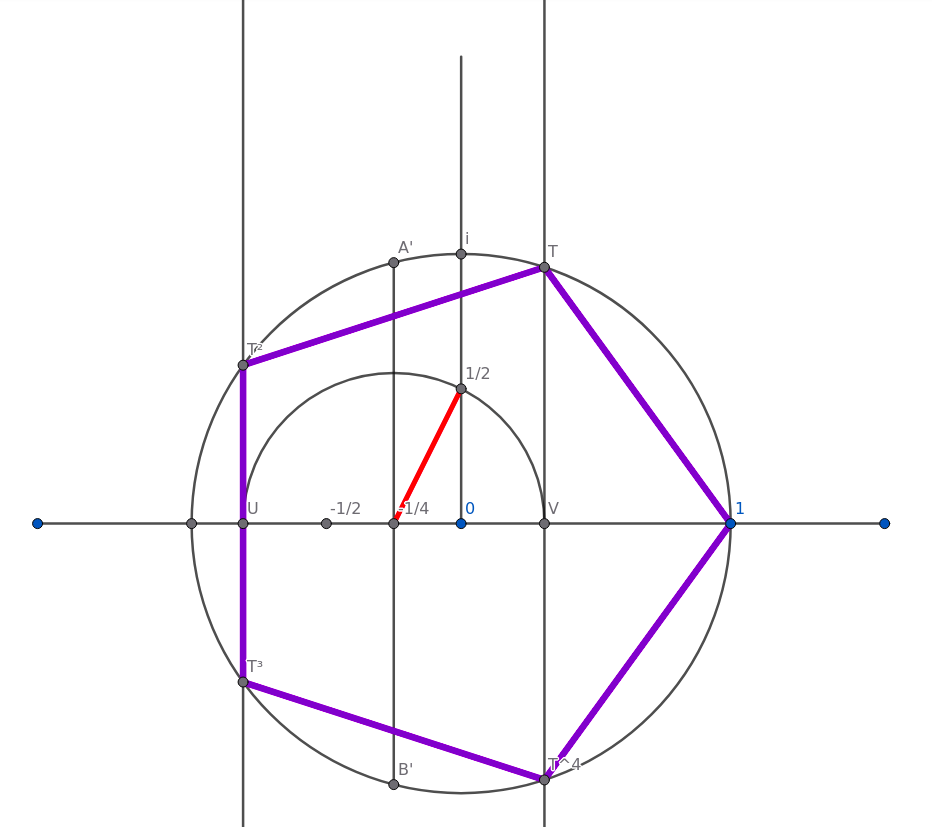
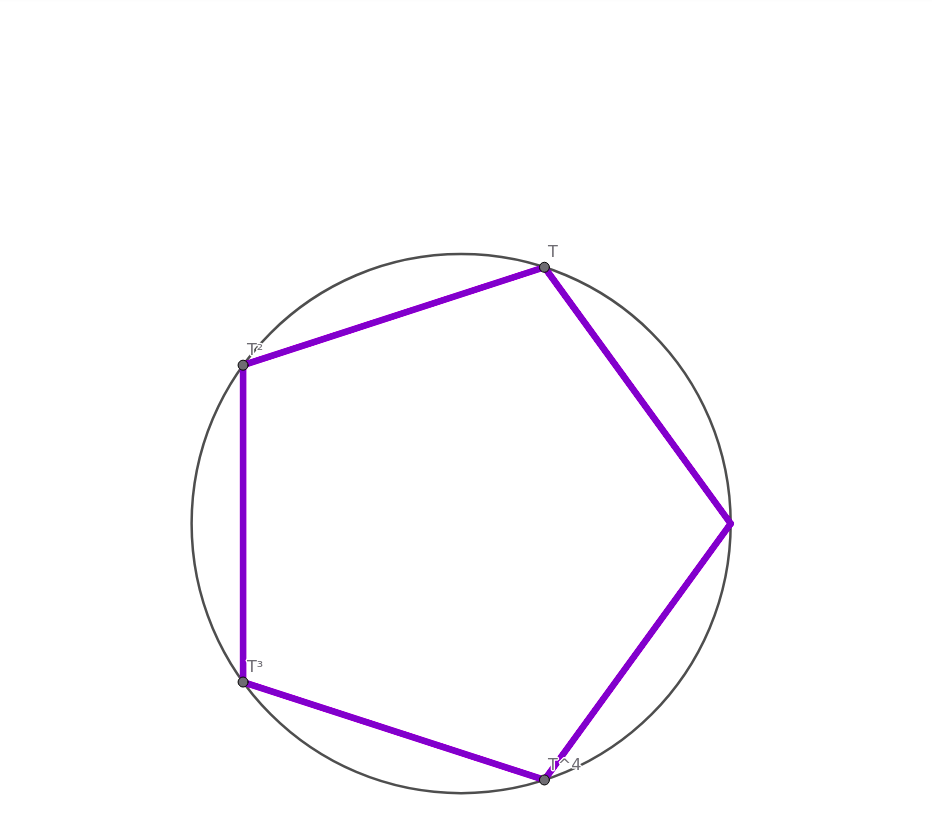
These are the X coordinates of the vertices of our regular pentagon!
Now if we draw the perpendiculars at those points, the places where
they meet the circle will form our regular pentagon.

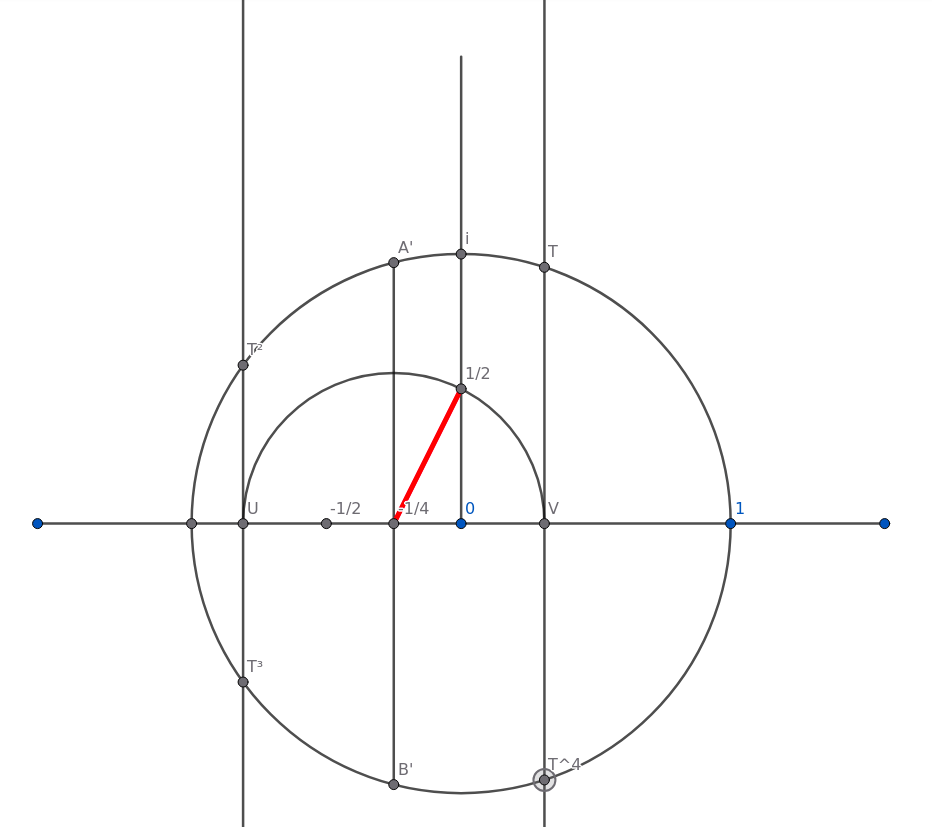
(Figure 12)

And we know it must be so! We know for certain that this is,
indeed, a regular pentagon. Derived from the algebra and geometry
combined through the complex numbers.

(Figure 13)

(Figure 14)

References


Nothing here is new, and everything can be found with quick searches on
wikipedia (and other sites).

With regards the geometric approach to Complex Numbers, all the write-ups
I've found have expressed a desire for a square root of minus one, declared
that one exists, and then explored the consequences. In so doing they then
discover the geometric interpretation, but I have not yet seen the approach
of exploring multiplication as a dilation of the number line, exploring that in
its own right, and discovering that the square root of minus one emerges
naturally and "for free".

I'd be delighted to hear from anyone with any references to this approach.

So this is more of a "See Also" rather than "References" per se.

Here are some Wikipedia pages:

For the significantly more adventurous:


Author details


Colin Wright graduated in 1982 from Monash University, Melbourne,
Australia, with a B.Sc.(Hons) in Pure Mathematics, and went on to
receive his doctorate in 1990 from Cambridge University, England.
While at Cambridge he also learned how to fire-breathe, unicycle,
juggle and ballroom dance. Since then he has worked as a research
mathematician, a computer programmer, and an electronics hardware
designer, taking time to give presentations all over the world on
"Juggling - Theory and Practice", and other topics.

He is now a full-time, freelance science and maths communicator.

Email: maths@solipsys.co.uk
Mastodon:


Incoming feedback ...

────────────────────────────────────────────────────────────────────────────────────────────────────
────────────────────────────────────────────────────────────────────────────────────────────────────
gjm @gjm 2025-08-12 13:56

@ColinTheMathmo Some rather superficial remarks.

You mention "complex analysis" without defining it, at a time when implicitly you're addressing
people who aren't very familiar with this stuff. Dunno whether it's worth adding a parenthesis or
not.

You define your thing called T and remark that its powers T2,T3,T4 are roots of the same polynomial,
and then say "These will form the vertices of a regular pentagon!" -- but you need 1 as well, and
it's not until a couple of paragraphs later that you explicitly say that 1 is a root of the
polynomial. I think a little reorganization around here might help.

When factoring x4+x3+x2+x+1 as the product of quadratics, it isn't immediately obvious to me that
"the leading terms and constant terms must all be 1" just by "symmetry". Why couldn't you have
(x2+ax−1)(x2+bx−1) ?

(I think an amateur audience will mostly not see even why you couldn't have 2s cancelling out 1/2s
or whatever, actually.)

The appeal to "symmetry" to say that "the other solution" to a2−a−1=0 gives us b may also confuse
more than it enlightens, especially as it's quite a different sort of symmetry from the one appealed
to before.

You say "We have found the Golden Ratio!", tell readers not to worry if they don't know about it,
... and a few paragraphs later start writing φ with the assumption that readers will understand what
it refers to. Maybe be more explicit?

Since you're writing for an audience that has never encountered complex numbers before, I don't
think you can get away with (1) expecting them to recognize immediately that √(φ2−4) is imaginary or
(2) using the Re(...) notation without explanation.

[1/?]

ID 115016139405663568 ↲ In reply to 115015501292492715
────────────────────────────────────────────────────────────────────────────────────────────────────
gjm @gjm 2025-08-12 14:08

@ColinTheMathmo "Working through the algebra with b instead of a, we use −1/φ instead of φ ..." -- I
am pretty sure your intended audience will have absolutely no idea where −1/φ comes from.

In the geometrical construction that follows, you generally don't explain _why_ a given thing you've
constructed is, say, i or 1/4 or whatever. Maybe that's OK; it's not generally very difficult to
figure out. But it should be a deliberate choice if so.

You refer to the point (0,1) as i but to the point (0,1/2) as 1/2. I think you should be consistent
about this.

After constructing the x-coords of your pentagon vertices, you say "Now if we the perpendiculars at
these points, the places where they meet the circle ...". Trivial problem: you accidentally a word.
Less trivial problem: you haven't explicitly said how to a perpendicular at a given point. You
probably should, or at least explain how one of the constructions you've already done generalizes.

Some less superficial concerns:

You start off by talking about compass-and-straightedge constructions. And then you start doing
algebra. And then you pull out of a hat a compass-and-straightedge construction that implements the
algebra you did.

There is, as I am sure you know very well, a general theorem saying that what you can do with
straightedge and compass is exactly what you can do by solving quadratics. It seems like that's
worth saying out loud at some point.

[2/?]

ID 115016183582761860 ↲ In reply to 115016139405663568
────────────────────────────────────────────────────────────────────────────────────────────────────
gjm @gjm 2025-08-12 14:17

@ColinTheMathmo When introducing numbers-as-transformations, you make a contrast with "taking
multiple copies" and emphasize that this _doesn't_ give you commutativity for free. That's not
wrong, but it's not like the "taking multiple copies" gives you commutativity for free either, and
scaling operations do commute with one another, so something in the emphasis here seems odd to me.

You explain what squaring is, then briefly what square-rooting is, and then ask what multiplication
by -1 is. This is all exactly what I'd expect to see if you'd previously said something like "We
will find it necessary to work with a kind of number that allows us to take a square root of -1",
but you haven't, and I think your intended not-very-expert audience will be somewhat confused about
where you're going and why.

I think it's absolutely fine _not_ to say at the outset that you're aiming at a square root of -1!
But in that case I think you should organize things a bit differently. Talk about scaling by numbers
like 2 and 3. Then (_before_ talking about square roots) explain that this works for negative
numbers too, and maybe show how multiplying by 2 and then by -3 gives you the same as multiplying by
-6 or something. And then ask: Can you think of a transformation that, when you do it twice,
multiplies by -1? and then pull the rabbit out of the hat, and emphasize (perhaps after talking a
bit about adding and subtracting etc.) that what you have just done is to create an extended notion
of numbers in which negative numbers have square roots.

(This isn't very different from what you've done, of course. But I think the differences are
improvements.)

[3/?]

ID 115016218962992903 ↲ In reply to 115016183582761860
────────────────────────────────────────────────────────────────────────────────────────────────────
gjm @gjm 2025-08-12 14:25

@ColinTheMathmo You say you aren't aware of any write-up of the geometric approach to complex
numbers, which surprises me -- I thought it was pretty standard. There's a very brief version at
https://plus.maths.org/content/maths-minute-complex-numbers and a longer one at
https://galileo.phys.virginia.edu/classes/152.mf1i.spring02/ComplexNumbers.htm -- these are the
first two I happened to find, and probably there are better ones out there.

A pedantic quibble: you describe rotation through 90 degrees and call it "in a very real sense, the
square root of minus one". It's _a_ square root of −1 and the fact that you can rotate in either
direction is a nice easy way to see why there are two equally good ones. This seems like it might be
worth mentioning, and if not might at least be worth acknowledging somehow.

When you start talking about rotations through a fifth of a turn, I think there might be some value
in reminding your readers that the goal was something to do with pentagons -- since that's the
actual reason for being interested in rotations of that size.

One final remark: I had always thought it was Gauss who figured out exactly which numbers are
constructible -- and maybe he did, but he didn't publish his proof that the condition is necessary
as well as sufficient, whereas Wantzel did. So I learned something from reading this :-).

[4/4]

ID 115016252612889543 ↲ In reply to 115016218962992903
────────────────────────────────────────────────────────────────────────────────────────────────────
Colin the Mathmo @ColinTheMathmo 2025-08-12 15:46

Comment about the Plus Maths article ... yes, it deals with the geometrical interpretation, but it
starts by conjuring "i" into existence from nothing, works through the algebra, and then interprets
it. I should make that clearer.

ID 115016571784335234 ↲ In reply to 115016252612889543
────────────────────────────────────────────────────────────────────────────────────────────────────


Backlinks: Home