Multiplex
Multiplex Pattern |
|
|
 Multiplex |
There are, however, many other ways of multiplexing. The following example is probably the easiest way to juggle 5 balls (short of putting them in a bag and tossing that up and down ...)
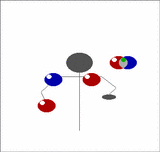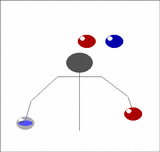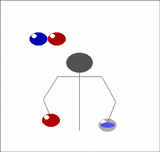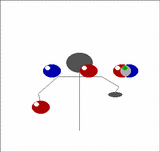
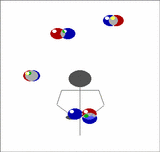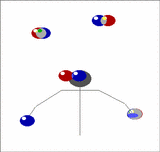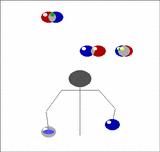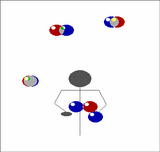
Imagine holding two balls in your left hand, one in the right, and having a pair of balls descending in front of you. Toss the two out of the left hand from a position just outside shoulder width so that they will come down in the middle, then of the two that are already descending in the middle, catch one in each hand. Now you have two in the right and one in the left. As the recently thrown pair start to come down repeat the above, but tossing the balls now from the right.
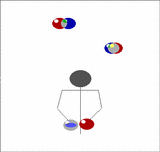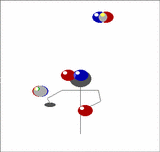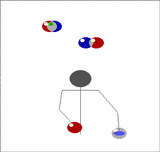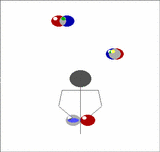 | We can generalise this. Imagine now that instead of one pair of balls descending in front of you that there's a whole stack of them. Toss the pair you are currently holding onto the top of the stack, then catch the bottom two, one in each hand, just as before. In this way you can juggle any odd number of balls, just by adding more pairs. |
 |
There is a version of the Site Swap Juggling Notation that covers Multiplex. In it, the throw of more than one ball is shown in square brackets containing regular Site Swap numbers. For example, [33] is the multiplex Site Swap for juggling six balls in a regular cascade, each throw being of two balls that travel together. 33[33] is the multiplex Site Swap for juggling four balls in a cascade, two of them travelling together as one. The above 5-ball pattern is usually described as [32] with the 2 being thrown in each case.
The multiplex extension to Site Swap can also be combined with the notation for Synchronous Site Swap. A more accurate description of the above 5-ball multiplex is then given as ([44x],2)(2,[44x]) with the 2 being held, as is more usual. Perhaps, however, it's easier to call it [23] and simply comment that the 2s are thrown.
ContentsThere were no headingsin the main text so there is no table of contents. |
Links on this page |
|
 Suggest a change ( <--
What does this mean?) /
Send me email
Suggest a change ( <--
What does this mean?) /
Send me email|
|
Quotation from Tim Berners-Lee |
|