Linear Programming Example

AllPages RecentChanges Links to this page Edit this page Search Entry portal Advice For New Users

A farmer has 90 acres on which he may raise peanuts and corn.

He has accepted orders requiring at least 10 acres of peanuts and 5 acres of corn.

He also must follow a regulation that the acreage for corn must be at least twice the acreage for peanuts.

If the profit is $100 per acre of corn and $200 per acre of peanuts, how many acres of each will give him the greatest profit?

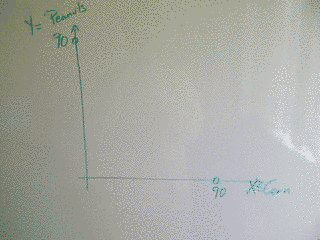
We want to know the acreage for corn and the acreage for peanuts. Let's represent them by X and Y: X = acres of corn Y = acres of peanuts Shown at right is our graph to start with:

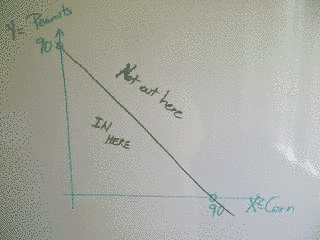
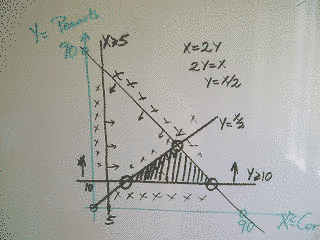
We are told that he has 90 acres in all, so we know that X+Y <= 90. That's a constraint.

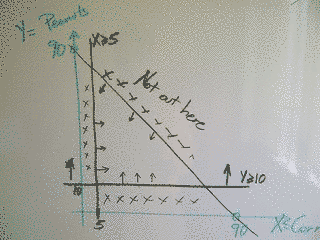
We are told that his orders require at least 10 acres of peanuts, so Y >= 10. We are also told that his orders require 5 acres of corn, so X >= 5 (remember, X is corn)

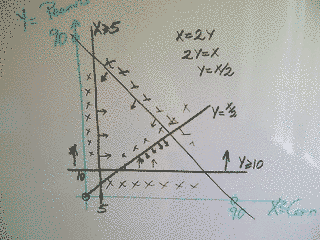
The next constraint is that the regulations state that the acreage for corn must be at least twice the acreage for peanuts. That means that X >= 2Y

Now we know we are inside this area. I've marked the corners because the basic theorem, the most fundamental fact in Linear Programming is this: The answer is always at a corner of the permitted region.

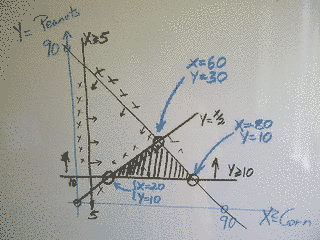
So we solve the equations to find the corners, and we get three solutions: So: X=20, Y=10 X=60, Y=30 X=80, Y=10 You should check that all the constraints are met by these solutions.

The final step, get the maximum profit.

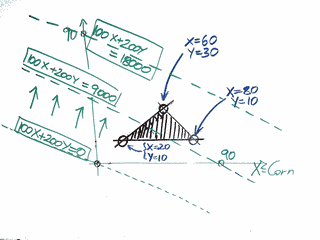
We know that the profit is 100X + 200Y. Which of these solutions gives the most profit, and how much profit does he make? One thing we can do is simply evaluate the objective function at each vertex of the region. The other thing is we can plot 100X+200Y=C for various values of C. Different values of C give parallel lines, and our objective is to get C as large as possible while still having the line intersect the area. Here we've plotted the lines for C=0, C=9000 and C=18000. See how as C increases the line moves up and to the right. C=18000 clearly has the line moved too far, so we need to work out the last place the line touches in the region as the line moves. That point is where X=60 and Y=30. If the line had a different slope then it might last touch somewhere else.