The Doodle Theorem, and beyond ...

A Simple Game

There's a game many children are introduced to, one way or another. It takes several forms - one is this:

Here's a drawing - see if you can reproduce it without going over any lines you've already drawn, and without lifting your pencil from the paper.

As it happens, this was exactly the challenge that faced the residents of Koenigsberg centuries ago: Could they take their Sunday afternoon stroll, crossing every bridge exactly once?

Some have it that the puzzle required that they return to their point of embarkation, others didn't add that extra condition, but over time all the residents came to agree that it was impossible.

And that's where normal people leave this sort of puzzle. They try for ages, decide they can't do it, and put it down. On the other hand, mathematicians then take up the challenge: Is it really impossible?

Can we prove it to be impossible?

That was done, as many readers will know, by Euler (pronounced "Oiler") in the 1700's, and is marked by some as the birthplace (birthtime?) of Graph Theory. Euler reasoned that if it was possible to walk about and cross every bridge exactly once, then every piece of land you visited has to have an even number of bridges - one to enter and one to exit for every time you visited. The plan of Koenigsberg, however, clearly shows that every piece of land has an odd number of bridges. So it is clearly impossible.

And so it is when trying to reproduce a drawing. To be able to draw the diagram without retracing lines, and in a single continuous stroke, every vertex, every meeting place, must have an even number of lines entering it. If not we will enter and depart some number of times, and finally enter and have no way out.

Of course, it's OK for the starting point and ending point to have an odd number of lines, but those are the only two. We can see from this diagram that we must start at one of the bottom two points and end at the other, but every other vertex (meeting place) has an even number of lines, and so it must be OK.

Have you seen the trap? I'll give you a moment. It's subtle until you see it, and some people still don't really understand, even when it's pointed out.

Have you seen it? Take a moment.

So what is the trap? I have followed in Euler's steps and shown that if a diagram can be drawn then all but at most two of the vertices must have an even number of lines.

I then asserted - without proof - that the converse was true. I said that if every vertex has an even number of lines meeting it, then it will be drawable.

"Well," say many people, "It's obvious, isn't it. With an even number at every vertex, every time you enter you can leave again, so nothing can go wrong. Only stands to reason."

Ah, but it's not true. Even though most people get left with the impression that this is true, and most of the time when this is shown to children the implication is obvious, it is not true.

At this point some of you will be spluttering, but others will be nodding along. Here is an example of a diagram where all the vertices have even degree (an even number of lines) and yet it cannot be drawn in a single stroke:

Now some people complain at this point that I've tricked them, and of course they were only thinking of connected examples. Well, fair enough, if you were only thinking of connected examples then maybe it is true. But is it? Really? How do you know?

And that's where we need to have a proof. So here's a conjecture:

• A connected network such that every vertex has even degree can be completely traversed in a single journey without retracing paths, and returning to the starting point.

Now, you'll notice here that I've added the condition of returning to where we started, because that now means that we can't have the alternate condition of two vertices having odd degree. It just makes life simpler, and it's not hard to prove the more general case from this one.

So how do we prove this? There are several proofs, and preferences differ as to which people think is the easiest and cleanest. The one I like is this. Take a walk, and return to where you started. You never get stuck when you do this, because at each vertex you use lines in pairs, so every time you come in, there's always a way out. If you covered every path, you're done.

If not, do it again, but when you come across one of the paths you didn't take, take that one as a diversion, and wander about on paths you didn't take the first time until you return to that branch point, and then complete your original journey. You've now covered more of the network. Keep doing this, keep augmenting your journey, until finally you've covered everything.

That's not a formal proof, but it gives the right idea. You need to check that the things I've told you to do are always possible, but that's not too hard.

So in this case the converse is true:

You can draw the diagram if and only if every vertex has even degree.

It's interesting to note that neither the statement nor the proof actually require that the network be drawn on a plane as a diagram. It's true for networks in general, which is nice. But now, let's consider the case where it is drawn on a plane. Here's an example:

Every vertex has even degree, so we can draw this, returning to our starting point, without retracing steps, and without retracing a line we've already drawn.

Adding a twist

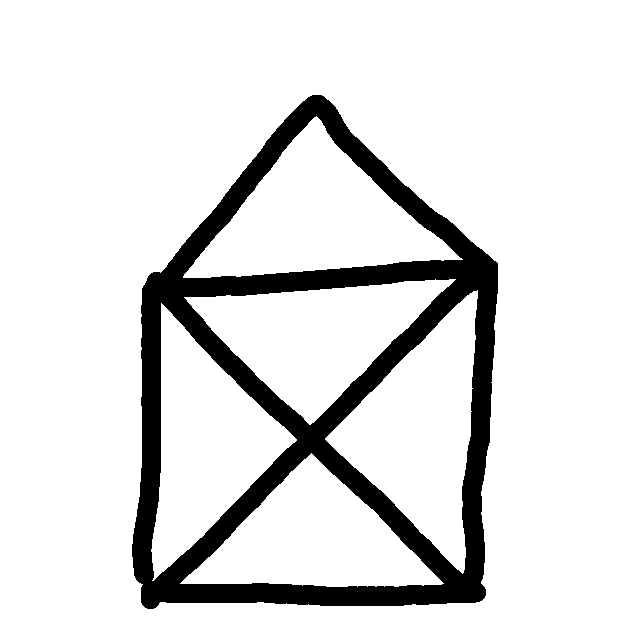
Claim: We can draw this in a single pencil line without crossing over a line we've already drawn.

Try it. Here's an example where it's gone wrong:

In this attempt we've made a good start, but got ourselves into a position where as we approach the next vertex we can see that we will have to cross over a line we've already drawn. So that's not allowed.

Is it possible? Try for yourself ...

Again, if any vertex has an odd degree then we won't be able to do this, but now the claim is that the converse holds, and it's no longer quite so obvious. A few examples and you might convince yourself that it works, but just because it works on a few examples, that doesn't mean it's always true. So is it always true?

Can we make every vertex look something like this?

Really?

Well, yes, we can make every vertex look something like that, and the proof is quite similar to the one we gave above for the original statement. We won't go into it here, we'll leave that as an exploration for the interested reader.

A different challenge

You will find - I claim - that every doodle can be coloured like this using just two colours. Try it. Again, try a few examples. Get someone else to draw a doodle, and try to colour that. Try to draw one that can't be coloured.

You'll find that you can't, no matter how hard you try.

Claim: Every doodle can be two-coloured.

Again, at this point normal people will say "Huh. That's curious." and then move on. Mathematicians, on the other hand, will wonder why this is true. Indeed, they will start by wondering whether it is true. Sure, it worked for all the small examples they tried, but what if there's a doodle with a million billion regions - will it still work for that?

Good question.

Yes.

Here's a proof. We've already seen (although not proved here) that any doodle can be drawn in a single, continuous pencil stroke such that:

• No line is retraced
• We finish where we start
• We never cross over a line we've already drawn.

That means the vertices can be sort of "exploded" into small regions of their own, and the path enters and exits the region without ever touching the other parts of the path that visit that vertex. Now the doodle is a simply a distorted circle, and that means it has an inside, and an outside. We can shade the inside, and now we have a two-colouring of the original doodle.

Into the unknown

Of course, colouring regions like this restricts us to living in the plane, but there's a way that we can release ourselves from this limitation. What we do is think of the regions on the doodle as countries, and put a capital city in each country. Then if two countries share a border, we join their respective capitals with a road. In this way we end up with a new network, a network of roads. Colouring the regions corresponds to colouring the capitals, and the rule is now that if two capitals are joined by a road then they must get different colours. Here we can see a general example, not just one that's made from a doodle:

So now we have a new network, and we are colouring the vertices. The reason this is useful is that networks are not limited to living in the plane. The problem is that we have lost our proof that certain networks/doodles are two-colourable.

But we can rescue that. In our new network, imagine moving from vertex to vertex, travelling around the network and returning to where we started. If the network vertices can be two-coloured (and remember, they correspond to the regions in the original doodle) then we must alternate colours: black, white, black, white, and so on. So any wandering around the new network must consist of an even number of steps.

So now we have a simple way of deciding whether of not a network can have its vertices two-coloured: Check to see if every circuit is of even length. That sounds like a huge job, but actually there is a really easy way of doing it. Colour one vertex red, then all its neighbours green, then all their neighbours red, and so on. If you succeed then you've proved that all the circuits are of even length, because when you traverse a circuit you keep alternating colour.

But if that process goes wrong it's easy enough to show that there must be an odd length circuit. We'll leave that as an exercise for the dedicated individual.

So where is this pot of gold?

So we have seen that there is an easy way to see if a network can be drawn without lifting the pencil off the paper. The same test, whether every vertex is of even degree, even works for networks not necessarily limited to the plane.

We've also see that there is an easy way to see if a network can have its vertices two-coloured - it's possible if and only if every circuit is of even length, and we can test that just by trying it! If it fails, we find an odd length circuit. If it succeeds then, well, it's succeeded.

So there is a simple test to see if we can visit every edge of a network, and there is a simple test to see if we can two-colour the vertices of a network.

What next?

Well, we can ask if there is a simple test to see if we can visit every vertex of a network. Or we can ask if there is a simple test to see if we can three-colour the vertices of a network.

And here is the fun part: No one knows.

The first question - to visit every vertex - is called finding a Hamilton Cycle, and we know of no easy way either to find one, or to prove that there isn't one. The second question is simply called three colouring, and there is no efficient way of knowing whether an arbitrary network can be three coloured or not.

People have investigated these questions for a long time, and there is something really cool that they have discovered. If you can solve one of those problems, you can use it to solve the other. So in some sense these two problems, even though they look totally different, are kind of the same problem.

And there's more. Solving one of these, or any of hundreds like them, or proving that no such solution exists, is one of the Millennium Problems published by the Clay Mathematics Institute, and for which they have offered a one million dollar prize.

Well, that escalated quickly.